��Ŀ����
����Ŀ��ij��ҵһ���в�ͬʱ�̵��õ���![]() (��ǧ��ʱ)����ʱ��
(��ǧ��ʱ)����ʱ��![]() (Сʱ,
(Сʱ,![]() )�ĺ���
)���![]() ��������
��������![]() ,��ͼ�Ǻ���
,��ͼ�Ǻ���![]() �IJ���ͼ��(
�IJ���ͼ��(![]() ��Ӧ�賿
��Ӧ�賿![]() ��).
��).

(��)����ͼ��,��![]() ��ֵ��
��ֵ��
(��)���ڵ��ض�����������,�ӻ����ĽǶ�,��Ҫ���ƻ������糧���ŷ���,������Ӧ���ޣ���Ҫ������ҵ���ŷ���,������Ҫ�Ը���ҵʵ�з�ʱ��բ���ʩ.��֪����ҵij��ǰ�����ܷ��䵽�Ĺ�����![]() (��ǧ��ʱ)��ʱ��
(��ǧ��ʱ)��ʱ��![]() (Сʱ)�Ĺ�ϵ�������Ժ���ģ��
(Сʱ)�Ĺ�ϵ�������Ժ���ģ��![]() ģ��.��������С�ڸ���ҵ���õ���ʱ,��ҵ�ͱ���ͣ��.����Ԥ��ͣ��ʱ��������11�㵽12���,Ϊ��֤����ҵ�ȿ���ǰ��Ӧ��ͣ��,�ֿɾ�������ͣ��ʱ��,����������Ԥ�Ƶ�ʱ��ο�ʼ,�ö��ַ�����������ȷ��15���ӵ�ͣ��ʱ���.
ģ��.��������С�ڸ���ҵ���õ���ʱ,��ҵ�ͱ���ͣ��.����Ԥ��ͣ��ʱ��������11�㵽12���,Ϊ��֤����ҵ�ȿ���ǰ��Ӧ��ͣ��,�ֿɾ�������ͣ��ʱ��,����������Ԥ�Ƶ�ʱ��ο�ʼ,�ö��ַ�����������ȷ��15���ӵ�ͣ��ʱ���.
���𰸡�(��) ![]() ��(��) 11��15�ֵ�11��30��֮��.
��(��) 11��15�ֵ�11��30��֮��.
��������
(��)����ͼ�����ֵ��![]() �������������
�������������![]() ��������������
��������������![]() ��ֵ��(��)��
��ֵ��(��)��![]() ����
����![]() ����
����![]() Ϊ����ҵ��ͣ��ʱ�䣬��֪
Ϊ����ҵ��ͣ��ʱ�䣬��֪![]() ��
��![]() ���ǵ�������������ȷ��
���ǵ�������������ȷ��![]() �Ӷ��ɵý��.
�Ӷ��ɵý��.
(��)��ͼ��֪T=2(12-6)=12,�Ӷ���=![]() =
=![]() ,
,
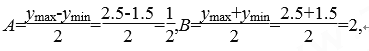
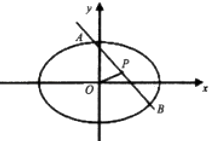
����![]()
����(0,2.5)�æ�=![]() +2k��,kZ,
+2k��,kZ,
��Ϊ0<��<��,
���Ԧ�=![]() .
.
(��)��(��)֪![]()
��![]()
��h(t0)=0,��t0Ϊ����ҵ��ͣ��ʱ��.
��֪h(t)��(11,12)���ǵ�����������.
��h(11)=f(11)-g(11)<0,h(12)=f(12)-g(12)>0,
��![]() ,
,
����t0(11,11.5),��11�㵽11��30��֮��(����15����),��h(11.25)=f(11.25)- ![]()
����t0(11.25,11.5),��11��15�ֵ�11��30��֮��(ǡ��15����),
���Թ�����11��15�ֵ�11��30��֮���ʱ���ͣ��.

 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�����Ŀ��ͨ�����ѯ��110���Ա�ͬ�Ĵ�ѧ���Ƿ�ij���˶����õ����µ���������
�� | Ů | �ܼ� | |
���� | 40 | 20 | 60 |
������ | 20 | 30 | 50 |
�ܼ� | 60 | 50 | 110 |
�� ![]() ��ã�
��ã� ![]() ��
��
P��K2��k�� | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
���ո������õ�����ȷ�����ǣ� ��
A.�ڷ�����ĸ��ʲ�����0.1%��ǰ���£���Ϊ�����ø����˶����Ա��йء�
B.�ڷ�����ĸ��ʲ�����0.1%��ǰ���£���Ϊ�����ø����˶����Ա��ء�
C.��99%���ϵİ�����Ϊ�����ø����˶����Ա��йء�
D.��99%���ϵİ�����Ϊ�����ø����˶����Ա��ء�