题目内容
【题目】已知二次函数![]() ,满足
,满足![]() ,
,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 内,求实数
内,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(Ⅰ)通过f(0)=2,求出c,利用f(x+1)﹣f(x)=2x﹣1,求出a,b,得到函数的解析式.
(Ⅱ)求出函数f(x)的对称轴,然后求解fmax(x),列出关系式即可求解实数t的取值范围为(﹣∞,5).
(Ⅲ)g(x)=x2﹣(2+m)x+2,若g(x)的两个零点分别在区间(﹣1,2)和(2,4)内,利用零点存在定理列出不等式组求解即可.
解:(Ⅰ)由f(0)=2,得c=2,
又f(x+1)﹣f(x)=2x﹣1,得2ax+a+b=2x﹣1,
故![]() ,解得:a=1,b=﹣2,
,解得:a=1,b=﹣2,
所以f(x)=x2﹣2x+2.
(Ⅱ)f(x)=x2﹣2x+2=(x﹣1)2+1,对称轴为x=1∈[﹣1,2],
又f(﹣1)=5,f(2)=2,所以fmax(x)=f(﹣1)=5.
关于x的不等式f(x)﹣t>0在[﹣1,2]有解,则t<f(x)max=5,
所以实数t的取值范围为(﹣∞,5).
(Ⅲ)g(x)=x2﹣(2+m)x+2,若g(x)的两个零点分别在区间(﹣1,2)和(2,4)内,
则满足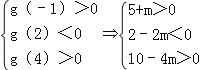
解得:![]() ,所以实数m的取值范围为
,所以实数m的取值范围为![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目