题目内容
【题目】已知圆C与x轴相切，圆心C在射线3x﹣y=0（x＞0）上，直线x﹣y=0被圆C截得的弦长为2 
（1）求圆C标准方程；
（2）若点Q在直线l1：x+y+1=0上，经过点Q直线l2与圆C相切于p点，求|QP|的最小值．
【答案】
（1）解：因为圆心C在射线3x﹣y=0（x＞0）上，
设圆心坐标为 （a，3a），且a＞0，
圆心（a，3a）到直线x﹣y=0的距离为 
又圆C与x轴相切，所以半径r=3a
设弦AB的中点为M，则|AM|= 
在RtAMC中，得 
解得a=1，r2=9
故所求的圆的方程是（x﹣1）2+（y﹣3）2=9
（2）解：如图，
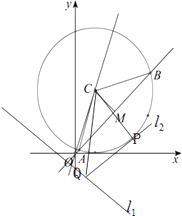
在Rt△QPC中，|QP|= 
，
所以，当|QC|最小时，|QP|有最小值；
所以QC⊥l1于Q点时，|QC|min= 
= 
所以，|QP|min= 
【解析】（1）设圆心坐标为 （a，3a），且a＞0，求出圆心（a，3a）到直线x﹣y=0的距离，利用勾股定理，求出圆心与半径，即可求圆C标准方程；（2）在Rt△QPC中，|QP|= ，所以，当|QC|最小时，|QP|有最小值．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】2012年，商品价格一度成为社会热点话题，某种新产品投放市场的100天中，前40天价格呈直线上升，由于政府及时采取有效措施，从而使后60天的价格呈直线下降，现统计出其中4天的价格如下表
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格（元） | 23 | 30 | 22 | 7 |
（1）写出价格f（x）关于时间x的函数关系式（x表示投放市场的第x天）；
（2）销售量g（x）与时间x的函数关系： 
（1≤x≤100，且x∈N），则该产品投放市场第几天销售额最高？最高为多少元？
