题目内容
【题目】已知椭圆E: ![]() ,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.
,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列. 
(Ⅰ)求a,b,k的关系式;
(Ⅱ)若离心率 ![]() 且
且 ![]() ,当m为何值时,椭圆的焦距取得最小值?
,当m为何值时,椭圆的焦距取得最小值?
【答案】解:(Ⅰ)设A(x1 , y1),B(x2 , y2), 由直线OA,AB,OB的斜率依次构成等比数列,
得 ![]() ,
,
由 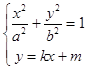 ,可得(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0,
,可得(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0,
故△=(2a2km)2﹣4(b2+a2k2)(a2m2﹣a2b2)>0,
即b2﹣m2+a2k2>0,
又x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
则 ![]() ,
,
即 ![]() ,
,
即 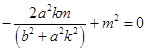 ,
,
又直线不经过原点,所以m≠0,
所以b2=a2k2即b=ak;
(Ⅱ)若 ![]() ,则
,则 ![]() ,
, ![]() ,
,
又k>0,得 ![]() ,
,
则x1+x2=﹣ ![]() =﹣
=﹣ ![]() m,x1x2=
m,x1x2= ![]() =
= ![]() m2﹣2c2 ,
m2﹣2c2 ,
|AB|= ![]()
![]() =
= ![]()
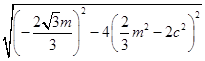
= ![]() ,
,
化简得 ![]() (△>0恒成立),
(△>0恒成立),
当 ![]()
【解析】(Ⅰ)设A(x1 , y1),B(x2 , y2),运用等比数列的中项的性质,以及联立直线方程和椭圆方程,运用韦达定理,化简整理,即可得到b=ak;(Ⅱ)运用离心率公式,可得斜率k,再由弦长公式,结合条件,运用基本不等式即可得到所求最值,以及m的取值.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目