Question

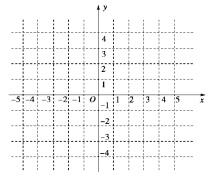
【题目】如图，定义在［－1,+∞)上的函数的图象由一条线段及抛物线的一部分组成．

(1)求的值及的解析式；

(2)若f（x）=，求实数x的值．

Answer 1

【答案】(1) f(f(4))=1,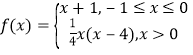 (2)

【解析】

（1）运用待定系数法设出解析式，再把已知点代入求解即可；

（2）分段求解，符合题意的保留，不符合题意的舍去．

（1）根据图象可知f（4）=0，∴f（f（4））=f（0）=1，

设y=kx+b

因为过点（0，1）和点（﹣1，0）代入可得：b=1，k=1

即y=x+1

当x≥0时，y=ax2+bx+c，

因为过点（0，0）（4，0）（2，﹣1）代入可得：

y=x2﹣x

所以；y=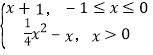

（2）f（x）=，

当x+1=时，x=﹣，符合题意；

当﹣x=时，即x=2，x=2（舍去）

故x=﹣，x=2