题目内容
【题目】某医科大学实习小组为研究实习地昼夜温差与患感冒人数之间的关系，分别到当地气象部门和某医院抄录了1月份至3月份每月5日、20日的昼夜温差情况与因患感冒而就诊的人数，得到如表资料：
日期 | 1月5日 | 1月20日 | 2月5日 | 2月20日 | 3月5日 | 3月20日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该小组确定的研究方案是：先从这六组数据中随机选取4组数据求线性回归方程，再用剩余的2组数据进行检验.
（1）求剩余的2组数据都是20日的概率；
（2）若选取的是1月20日，2月5日，2月20日，3月5日四组数据.
①请根据这四组数据，求出
关于
的线性回归方程
（
，
用分数表示）；
②若某日的昼夜温差为
，预测当日就诊人数约为多少人？
附参考公式：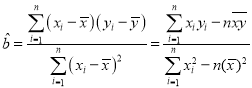
，
.
【答案】（1）
；（2）①
；②14人.
【解析】
（1）记六组依次为1，2，3，4，5，6，列出从这六组数据中随机选取4组数据后，剩余的2组数据所有可能的情况，同时得出剩余的2组数据都是20日的情况，计数后计算概率；
（2）根据所给数据计算
，然后计算回归方程中的系数，得回归方程，把
代入回归方程可得估计值．
（1）记六组依次为1，2，3，4，5，6，从这六组数据中随机选取4组数据后，剩余的2组数据所有可能的情况为：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共15种，其中2组数据都是20日，即都取自第2，4，6组的，，共3种，.
根据古典概型概率公式，剩余的2组数据都是20日的概率为：
；
（2）①由所选数据得
，
，
由参考公式得
，
则
.
所以
关于
的线性回归方程为.
②当时，
，
所以昼夜温差为
时，当日就诊人数约为14人.
【题目】改革开放以来，我国农村7亿多贫困人口摆脱贫困，贫困发生率由1978年的97.5%下降到2018年底的1.4%，创造了人类减贫史上的中国奇迹，为全球减贫事业贡献了中国智慧和中国方案．“贫困发生率”是指低于贫困线的人口占全体人口的比例．2012年至2018年我国贫困发生率的数据如下表：
年份（ | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
（1）从表中所给的7个贫困发生率数据中任选两个，求至少有一个低于5%的概率；
（2）设年份代码
，利用回归方程，分析2012年至2018年贫困发生率的变化情况，并预测2019年贫困发生率．
附：回归直线
的斜率和截距的最小二乘估计公式分别为：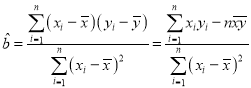
，
．
