题目内容
【题目】已知在平面直角坐标系
中， 
为坐标原点，曲线
： 
（
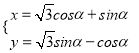为参数），在以平面直角坐标系的原点为极点， 
轴的正半轴为极轴，取相同单位长度的极坐标系，直线
： 
.
（Ⅰ）求曲线
的普通方程和直线
的直角坐标方程；
（Ⅱ）曲线
上恰好存在三个不同的点到直线
的距离相等，分别求出这三个点的极坐标.
【答案】（I）
， 
；（II）： 
、
.
【解析】试题分析：（1）平方相加消去参数
，即可得到曲线
的普通方程，利用两角和的正弦公式极坐标与直角坐标互化求出直线
的直角坐标方程；（2）求出圆的圆心与半径，求出三个点的直角坐标，然后利用互化公式可求解这三点的极坐标.
试题解析：（Ⅰ）曲线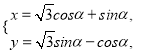
，
可得： 
曲线的普通方程
： 
.
直线
： 
.
直线
的直角坐标方程： 
.
（Ⅱ）∵圆
的圆心
半径为2，圆心
到直线的距离为1，
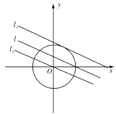
∴这三个点在平行直线
与
上，如图：直线
与
与
的距离为1.
： 
， 
： 
.
可得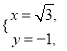
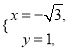
两个交点
；
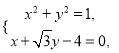
解得
，
这三个点的极坐标分别为： 
、
.
练习册系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
