题目内容
【题目】已知椭圆![]() 的短轴端点到右焦点
的短轴端点到右焦点![]() 的距离为2.
的距离为2.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() ,若
,若![]() ,
, ![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1) ![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(Ⅰ)利用椭圆的几何要素间的关系进行求解;(Ⅱ)联立直线和椭圆的方程,得到关于![]() 或
或![]() 的一元二次方程,利用根与系数的关系和平面向量的线性运算进行证明.
的一元二次方程,利用根与系数的关系和平面向量的线性运算进行证明.
试题解析:(Ⅰ)由题意有: ![]() ,且
,且![]() ,
,
所以![]() ,
, ![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由题意直线![]() 过点
过点![]() ,且斜率存在,设方程为
,且斜率存在,设方程为![]() ,
,
将![]() 代人得
代人得![]() 点坐标为
点坐标为![]() ,
,
由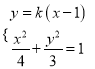 ,消元得
,消元得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() 且
且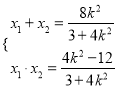 ,
,
方法一:因为![]() ,所以
,所以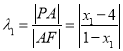 .
.
同理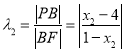 ,且
,且![]() 与
与![]() 异号,
异号,
所以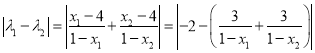

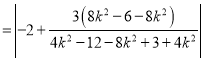
![]() .
.
所以, ![]() 为定值
为定值![]() .
.
方法二:由题意,当![]() 时, (若:不妨设
时, (若:不妨设![]() ,加一分)
,加一分)
有![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]()
所以![]() ,同理
,同理![]() .
.
从而![]()
![]()
![]()
![]() .
.
当![]() 时,同理可得
时,同理可得![]() .
.
所以, ![]() 为定值
为定值![]() .
.
方法三:由题意直线![]() 过点
过点![]() ,设方程为
,设方程为![]()
![]() ,
,
将![]() 代人得
代人得![]() 点坐标为
点坐标为![]() ,
,
由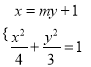 消元得
消元得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() 且
且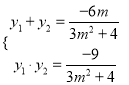 ,
,
因为![]() ,所以
,所以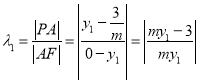 .
.
同理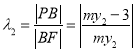 ,且
,且![]() 与
与![]() 异号,
异号,
所以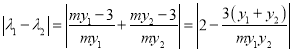
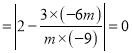 .
.
又当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() ,
,
所以, ![]() 为定值
为定值![]() .
.

【题目】2017年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如下表:
评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
评分类型 | D | C | B | A |
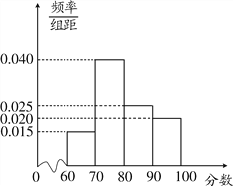 考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
(Ⅰ)评分类型为A的商业连锁店有多少家;
(Ⅱ)现从评分类型为A,D的所有商业连锁店中随机抽取两家做分析,求这两家来自同一评分类型的概率.
【题目】为预防H1N1病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如表:
A组 | B组 | C组 | |
疫苗有效 | 673 | x | y |
疫苗无效 | 77 | 90 | z |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知y≥465,z≥25,求不能通过测试的概率.