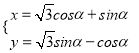题目内容
【题目】已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是( )
A.(1,+∞)
B.![]()
C.(1,3]
D.(1,5]
【答案】D
【解析】解:当a>1时,函数f(x)在(0,+∞)上单调递增,f(x)=ax﹣1>0;
当0<a<1时,函数f(x)在(0,+∞)上单调递减,f(x)=ax﹣1<0,舍去.
故a>1.
∵函数g(x)=f(x+1)﹣4的图象不过第二象限,
∴g(0)=a1﹣5≤0,
∴a≤5,
∴a的取值范围是(1,5].
故选:D.
对a分类讨论:利用指数函数的单调性可得a>1.由于函数g(x)=ax+1﹣5的图象不过第二象限,可得g(0)≤0,求解即可得答案.

练习册系列答案
相关题目