题目内容
求过两直线l1:x+y+1=0,l2:5x-y-1=0的交点，且与直线3x+2y+1=0的夹角为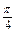
的直线方程.
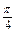的直线方程.所求直线方程为x+5y+5=0
设所求直线方程为x+y+1+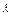
(5x-y-1)=0,
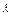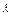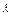即(1+5)x+(1-)y+1-=0.
因为所求直线与直线3x+2y+1=0的夹角为,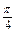
所以tan=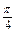
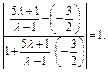
解得=-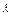
.
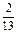∴所求直线方程为x+5y+5=0.
又直线l2:5x-y-1=0与直线3x+2y+1=0的夹角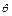
满足tan=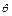
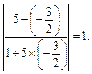
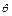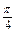∴=，故直线l2也是符合条件的一解.
综上所述，所求直线方程为
x+5y+5=0或5x-y-1=0.
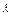(5x-y-1)=0,即(1+5
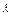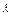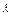)x+(1-)y+1-=0.因为所求直线与直线3x+2y+1=0的夹角为
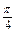,所以tan
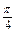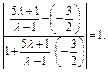
=解得
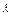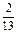=-.∴所求直线方程为x+5y+5=0.
又直线l2:5x-y-1=0与直线3x+2y+1=0的夹角
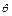满足tan=∴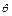
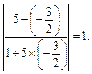
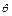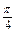=，故直线l2也是符合条件的一解.综上所述，所求直线方程为
x+5y+5=0或5x-y-1=0.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
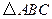的三个顶点的坐标分别为
，
，
．
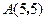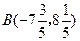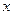轴上求一点
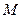，使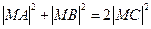
．
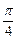后,所得的直线方程是
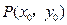且和直线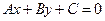
垂直的直线的方程．
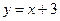与曲线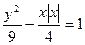
的交点的个数是 个．