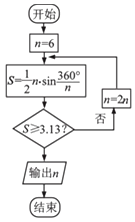
题目内容
【题目】某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格. (Ⅰ)设甲、乙两个班所抽取的10名同学成绩方差分别为 ![]() 、
、 ![]() ,比较
,比较 ![]() 、
、 ![]() 的大小(直接写出结果,不写过程);
的大小(直接写出结果,不写过程);
(Ⅱ)从甲班10人任取2人,设这2人中及格的人数为X,求X的分布列和期望;
(Ⅲ)从两班这20名同学中各抽取一人,在已知有人及格的条件下,求抽到乙班同学不及格的概率.
【答案】解:(Ⅰ)由茎叶图可得 ![]() .
.
(Ⅱ)由题可知X取值为0,1,2.
![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列为:
X | 0 | 1 | 2 |
P(X) | | | |
所以 ![]() .
.
(Ⅲ)由茎叶图可得,甲班有4人及格,乙班有5人及格.
设事件A=“从两班这20名同学中各抽取一人,已知有人及格”,
事件B=“从两班这20名同学中各抽取一人,乙班同学不及格”.
则在已知有人及格的条件下,抽到乙班同学不及格的概率:
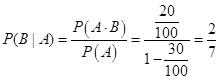 .
.
【解析】(Ⅰ)由茎叶图可得 ![]() .(Ⅱ)由题可知X取值为0,1,2.分另求出相应的概率,由此能求出X的分布列.(Ⅲ)由茎叶图可得,甲班有4人及格,乙班有5人及格.设事件A=“从两班这20名同学中各抽取一人,已知有人及格”,事件B=“从两班这20名同学中各抽取一人,乙班同学不及格”,由此利用条件概率计算公式能求出在已知有人及格的条件下,抽到乙班同学不及格的概率.
.(Ⅱ)由题可知X取值为0,1,2.分另求出相应的概率,由此能求出X的分布列.(Ⅲ)由茎叶图可得,甲班有4人及格,乙班有5人及格.设事件A=“从两班这20名同学中各抽取一人,已知有人及格”,事件B=“从两班这20名同学中各抽取一人,乙班同学不及格”,由此利用条件概率计算公式能求出在已知有人及格的条件下,抽到乙班同学不及格的概率.
【考点精析】解答此题的关键在于理解茎叶图的相关知识,掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少,以及对离散型随机变量及其分布列的理解,了解在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户,按年龄分组进行访谈,统计结果如表.
组号 | 年龄 | 访谈人数 | 愿意使用 |
1 | [18,28) | 4 | 4 |
2 | [28,38) | 9 | 9 |
3 | [38,48) | 16 | 15 |
4 | [48,58) | 15 | 12 |
5 | [58,68) | 6 | 2 |
(Ⅰ)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,则各组应分别抽取多少人?
(Ⅱ)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(Ⅲ)按以上统计数据填写下面2×2列联表,并判断以48岁为分界点,能否在犯错误不超过1%的前提下认为,是否愿意选择此款“流量包”套餐与人的年龄有关?
年龄不低于48岁的人数 | 年龄低于48岁的人数 | 合计 | |
愿意使用的人数 | |||
不愿意使用的人数 | |||
合计 |
参考公式: ![]() ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.
P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |