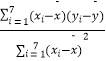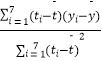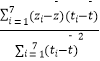题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)若![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)f(x)的值域为[0,4].(2)a的取值范围为![]() .
.
【解析】试题分析:(1)化简函数得f(x)=ln2x-2ln x+1,令t=ln x∈[-1,2],得y=t2-2t+1,根据二次函数性质求最值即可;
(2)由条件知ln2x-aln x-2a-1≤0恒成立,令t=ln x∈[-1,2],所以t2-at-2a-1≤0恒成立,利用二次函数性质,讨论单调性,只需ymax≤0即可.
试题解析:
(1)当a=1时,y=f(x)=ln2x-2ln x+1,
令t=ln x∈[-1,2],所以y=t2-2t+1=(t-1)2,
当t=1时,取得最小值0;t=-1时,取得最大值4
所以f(x)的值域为[0,4].
(2)因为f(x)≤-aln x+4,所以ln2x-aln x-2a-1≤0恒成立,
令t=ln x∈[-1,2],所以t2-at-2a-1≤0恒成立,设y=t2-at-2a-1,
所以当![]() ≤
≤![]() 即a≤1时,当t=2时ymax=-4a+3≤0,所以
即a≤1时,当t=2时ymax=-4a+3≤0,所以![]() ≤a≤1,
≤a≤1,
当![]() >
>![]() 即a>1时,当t=-1时ymax=-a≤0,所以a>1,
即a>1时,当t=-1时ymax=-a≤0,所以a>1,
综上所述,a的取值范围为![]() 。
。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某公司为确定下一年投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年利润y(单位:万元)的影响,对近5年的宣传费xi和年利润yi(i=1,2,3,4,5)进行了统计,列出了下表:
x(单位:千元) | 2 | 4 | 7 | 17 | 30 |
y(单位:万元) | 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合y与x的关系,请你建立y关于x的线性回归方程(系数精确到0.01);
(2)小李决定选择对数回归模拟拟合y与x的关系,得到了回归方程: ![]() =1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据
=1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据 ![]() (yi﹣
(yi﹣ ![]() i)2=1.15) 参考公式:相关指数R2=1﹣
i)2=1.15) 参考公式:相关指数R2=1﹣ 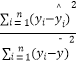
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为 ![]() =
= 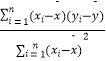 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x,参考数据:ln40=3.688,
x,参考数据:ln40=3.688, ![]() =538.
=538.
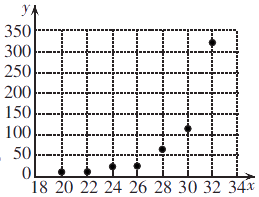
【题目】为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据列于下表中,并做出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈现线性相关关系,现分别用模型① ![]() 与模型;②
与模型;② ![]() 作为产卵数y和温度x的回归方程来建立两个变量之间的关系.
作为产卵数y和温度x的回归方程来建立两个变量之间的关系.
温度x/°C | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
产卵数y/个 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| | | |
26 | 692 | 80 | 3.57 |
| | | |
1157.54 | 0.43 | 0.32 | 0.00012 |
其中 ![]() ,
, ![]() ,zi=lnyi ,
,zi=lnyi , ![]() ,
,
附:对于一组数据(μ1 , ν1),(μ2 , ν2),(μn , νn),其回归直线v=βμ+α的斜率和截距的最小二乘估计分别为:  ,
, ![]()
(1)根据表中数据,分别建立两个模型下y关于x的回归方程;并在两个模型下分别估计温度为30°C时的产卵数.(C1 , C2 , C3 , C4与估计值均精确到小数点后两位)(参考数据:e4.65≈104.58,e4.85≈127.74,e5.05≈156.02)
(2)若模型①、②的相关指数计算分别为 ![]() .,请根据相关指数判断哪个模型的拟合效果更好.
.,请根据相关指数判断哪个模型的拟合效果更好.