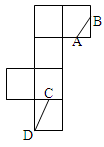
题目内容
在几何体ABCDE中,∠BAC=
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
(1)求证:DC∥平面ABE;
(2)求证:AF⊥平面BCDE;
(3)求证:平面AFD⊥平面AFE.

| π |
| 2 |
(1)求证:DC∥平面ABE;
(2)求证:AF⊥平面BCDE;
(3)求证:平面AFD⊥平面AFE.

(1)∵DC⊥平面ABC,EB⊥平面ABC,
∴DC∥EB,
又∵DC?平面ABE,
EB?平面ABE,
∴DC∥平面ABE,
(2)∵DC⊥平面ABC,∴DC⊥AF,
又∵AF⊥BC,
∴AF⊥平面BCDE,
(3)由(2)知AF⊥平面BCDE,
∴AF⊥EF,在三角形DEF中,由计算知DF⊥EF,
∴EF⊥平面AFD,又EF?平面AFE,
∴平面AFD⊥平面AFE.
∴DC∥EB,
又∵DC?平面ABE,
EB?平面ABE,
∴DC∥平面ABE,
(2)∵DC⊥平面ABC,∴DC⊥AF,
又∵AF⊥BC,
∴AF⊥平面BCDE,
(3)由(2)知AF⊥平面BCDE,
∴AF⊥EF,在三角形DEF中,由计算知DF⊥EF,
∴EF⊥平面AFD,又EF?平面AFE,
∴平面AFD⊥平面AFE.

练习册系列答案
相关题目
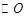 的直径AB=3,点C为
的直径AB=3,点C为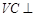 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点.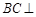 平面VAC;
平面VAC;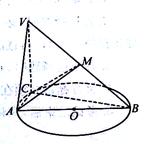
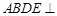 平面
平面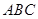 ,
,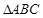 是等腰直角三角形,
是等腰直角三角形,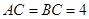 ,四边形
,四边形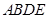 是直角梯形,
是直角梯形,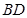 ∥AE,
∥AE,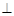
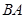 ,
,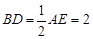 ,
,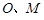 分别为
分别为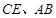 的中点.
的中点.
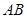 与
与 所成角的大小;
所成角的大小;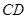 和平面
和平面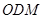 所成角的正弦值.
所成角的正弦值.