题目内容
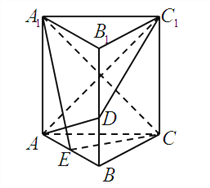
【题目】如图,正三棱柱![]() 的所有棱长均
的所有棱长均![]() ,
,![]() 为棱
为棱![]() (不包括端点)上一动点,
(不包括端点)上一动点,![]() 是
是![]() 的中点.
的中点.
(Ⅰ)若![]() ,求
,求![]() 的长;
的长;
(Ⅱ)当![]() 在棱
在棱![]() (不包括端点)上运动时,求平面
(不包括端点)上运动时,求平面![]() 与平面
与平面![]() 的夹角的余弦值的取值范围.
的夹角的余弦值的取值范围.
【答案】(Ⅰ)BD=1;(Ⅱ)(![]() ,
,![]() ].
].
【解析】【试题分析】(I)由![]() 得到
得到![]() 平面
平面![]() ,所以
,所以![]() ,由于
,由于![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,由此得到
,由此得到![]() 为
为![]() 的中点,所以
的中点,所以![]() .(I)以
.(I)以![]() 为空间坐标原点建立空间直角坐标系,利用两个平面的法向量来求得它们夹角的余弦值的取值范围.
为空间坐标原点建立空间直角坐标系,利用两个平面的法向量来求得它们夹角的余弦值的取值范围.
【试题解析】
证明:(Ⅰ),由AC=BC,AE=BE,知CE⊥AB,
又平面ABC⊥平面ABB1A1,所以CE⊥平面ABB1A1
而AD平面ABB1A1,∴AD⊥CE,又AD⊥A1C所以AD⊥平面A1CE,
所以AD⊥A1E.易知此时D为BB1的中点,故BD=1.
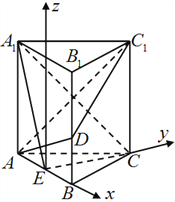
(Ⅱ)以E为原点,EB为x轴,EC为y轴,
过E作垂直于平面ABC的垂线为z轴,
建立空间直角坐标系,设BD=t,
则A(-1,0,0),D(1,0,t),C1(0,![]() ,2),
,2),
![]() =(2,0,t),
=(2,0,t),![]() =(1,
=(1,![]() ,2),设平面ADC1的法向量
,2),设平面ADC1的法向量![]() =(x,y,z),
=(x,y,z),
则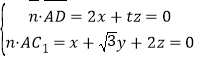 ,取x=1,得
,取x=1,得![]() ,
,
平面ABC的法向量![]() =(0,01),设平面ADC1与平面ABC的夹角为θ,
=(0,01),设平面ADC1与平面ABC的夹角为θ,
∴cosθ=![]() =
=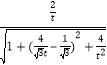 =
=![]() =
=![]()
由于t∈(0,2),故cosθ∈(![]() ,
,![]() ].
].
即平面ADC1与平面ABC的夹角的余弦值的取值范围为(![]() ,
,![]() ].
].

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目