题目内容
下列命题中,真命题是______.
①?x∈R,使得sinx+cosx=2;
②?x∈(0,π)有sinx>cosx;
③?ϕ∈R,使得f(x)=sin(ωx+ϕ)为奇函数;
④?a∈(-1,0),有1+a2<
.
①?x∈R,使得sinx+cosx=2;
②?x∈(0,π)有sinx>cosx;
③?ϕ∈R,使得f(x)=sin(ωx+ϕ)为奇函数;
④?a∈(-1,0),有1+a2<
| 1 |
| 1+a |
∵sinx+cosx=
sin(x+
)∈[-
,
],故①错误;
当x∈(0,
]时,sinx≤cosx,故②错误;
当φ=kπ,k∈Z时,f(x)=sin(ωx+φ)为奇函数,故③正确;
④当a∈(-1,0)时,a(a2+a+1)<0,即有a3+a2+a+1<1,则1+a2<
,故④正确;
故答案为:③④
| 2 |
| π |
| 4 |
| 2 |
| 2 |
当x∈(0,
| π |
| 4 |
当φ=kπ,k∈Z时,f(x)=sin(ωx+φ)为奇函数,故③正确;
④当a∈(-1,0)时,a(a2+a+1)<0,即有a3+a2+a+1<1,则1+a2<
| 1 |
| 1+a |
故答案为:③④

练习册系列答案
相关题目
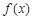 满足2
满足2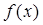 +
+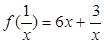 ,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,
,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,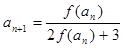 ,
,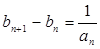 。
。 解析式;
解析式;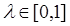 ,总存在自然数k,当n≥k时,
,总存在自然数k,当n≥k时,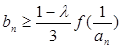 恒成立,求k的最小值。
恒成立,求k的最小值。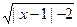 的定义域是(-∞,-1
的定义域是(-∞,-1 ∪[3,+∞
∪[3,+∞ .则 ( )
.则 ( )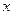 ,
, 且
且 ”是 ( )
”是 ( )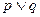 ”形式
”形式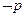 ” 形式
” 形式