题目内容
已知函数 满足2
满足2 +
+ ,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,
,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+, ,
, 。
。
(1)求函数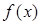 解析式;
解析式;
(2)求数列{an}、{bn}的通项公式;
(3)若对任意实数 ,总存在自然数k,当n≥k时,
,总存在自然数k,当n≥k时, 恒成立,求k的最小值。
恒成立,求k的最小值。
 满足2
满足2 +
+ ,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,
,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+, ,
, 。
。(1)求函数
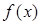 解析式;
解析式;(2)求数列{an}、{bn}的通项公式;
(3)若对任意实数
 ,总存在自然数k,当n≥k时,
,总存在自然数k,当n≥k时, 恒成立,求k的最小值。
恒成立,求k的最小值。(1)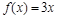
(2)
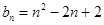
(3)3
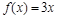
(2)

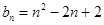
(3)3
解:(1)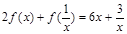 ,∴
,∴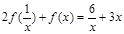 ,联立解得
,联立解得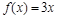
(2)∵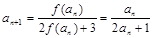 ,∴
,∴ ,
,
∴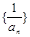 是以1为首项、2为公差的等差数列,
是以1为首项、2为公差的等差数列,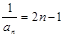 ,∴
,∴
又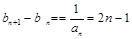
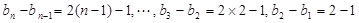 ,
,
相加有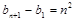 ,∴
,∴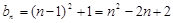
(3)对任意实数λ∈[0,1]时,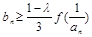 恒成立,
恒成立,
则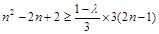 恒成立,变形为
恒成立,变形为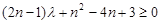 ,
,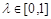 恒成立。
恒成立。
设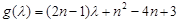 ,
,
∴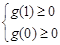 ,
,
∴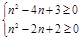 ∴
∴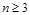 或
或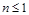 ,n∈N+
,n∈N+
故kmin=3
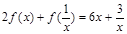 ,∴
,∴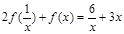 ,联立解得
,联立解得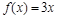
(2)∵
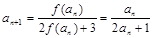 ,∴
,∴ ,
,∴
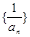 是以1为首项、2为公差的等差数列,
是以1为首项、2为公差的等差数列,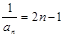 ,∴
,∴
又
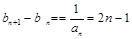
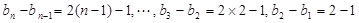 ,
,相加有
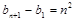 ,∴
,∴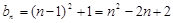
(3)对任意实数λ∈[0,1]时,
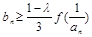 恒成立,
恒成立,则
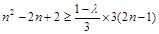 恒成立,变形为
恒成立,变形为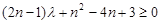 ,
,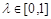 恒成立。
恒成立。设
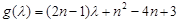 ,
,∴
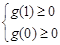 ,
,∴
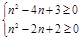 ∴
∴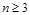 或
或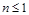 ,n∈N+
,n∈N+故kmin=3

练习册系列答案
相关题目
 )的围墙,且要求中间用围墙
)的围墙,且要求中间用围墙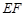 隔开,使得
隔开,使得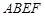 为矩形,
为矩形,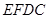 为正方形,设
为正方形,设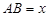 米,已知围墙(包括
米,已知围墙(包括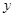 元。
元。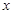 的函数解析式;
的函数解析式;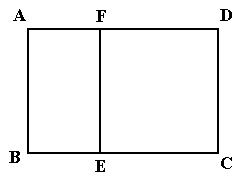
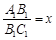 ,求公园ABCD所占面积S关于x的函数解析式;
,求公园ABCD所占面积S关于x的函数解析式;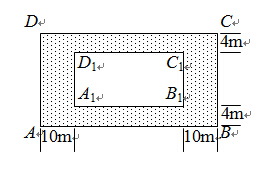
 ∈N*,定义
∈N*,定义 ,其中K是满足
,其中K是满足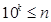 的最大整数,[x]表示不超过x的最大整数,如
的最大整数,[x]表示不超过x的最大整数,如 ,则(1)
,则(1) .
. 的最大整数m为 .
的最大整数m为 . ,函数
,函数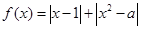 ,若
,若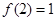 ,则
,则 .
.