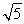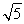题目内容
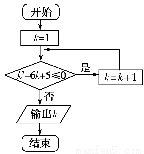
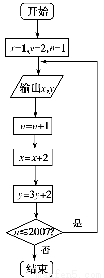
根据如图所示的程序框图,将输出的x,y值依次分别记为x1,x2,…,xk,…;y1,y2,…,yk,….
(1)分别求数列{xk}和{yk}的通项公式;
(2)令zk=xkyk,求数列{zk}的前k项和Tk,其中k∈N*,k≤2 007.
(1)yk=3k-1(k∈N*,k≤2 007).(2)(k-1)·3k+1+3+k2
【解析】(1)由框图,知数列{xk}中,x1=1,xk+1=xk+2,
∴xk=1+2(k-1)=2k-1(k∈N*,k≤2 007)
由框图,知数列{yk}中,yk+1=3yk+2,
∴yk+1+1=3(yk+1)∴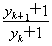 =3,y1+1=3.
=3,y1+1=3.
∴数列{yk+1}是以3为首项,3为公比的等比数列,
∴yk+1=3·3k-1=3k,∴yk=3k-1(k∈N*,k≤2 007).
(2)Tk=x1y1+x2y2+…+xkyk=1×(3-1)+3×(32-1)+…+(2k-1)(3k-1)=1×3+3×32+…+(2k-1)·3k-[1+3+…+(2k-1)]
记Sk=1×3+3×32+…+(2k-1)·3k ①
则3Sk=1×32+3×33+…+(2k-1)·3k+1 ②
①-②,得-2Sk=3+2·32+2·33+…+2·3k-(2k-1)·3k+1
=2(3+32+…+3k)-3-(2k-1)·3k+1=2×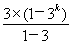 -3-(2k-1)·3k+1
-3-(2k-1)·3k+1
=3k+1-6-(2k-1)·3k+1=2(1-k)·3k+1-6
∴Sk=(k-1)·3k+1+3∴Tk=(k-1)·3k+1+3+k2

练习册系列答案
相关题目