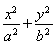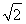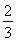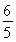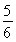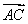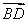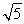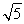Question

如图四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O是底面中心，A1O⊥底面ABCD，AB＝AA1＝.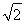

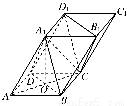
(1)证明：平面A1BD∥平面CD1B1；

(2)求三棱柱ABD－A1B1D1的体积．

 

Answer 1

（1）见解析（2）1.

【解析】(1)证明：由题设知，BB1綊DD1，

∴四边形BB1D1D是平行四边形，∴BD∥B1D1.

又BD?平面CD1B1，∴BD∥平面CD1B1.

∵A1D1綊B1C1綊BC，∴四边形A1BCD1是平行四边形，

∴A1B∥D1C.

又A1B?平面CD1B1，∴A1B∥平面CD1B1.

又BD∩A1B＝B，∴平面A1BD∥平面CD1B1.

(2)∵A1O⊥平面ABCD，

∴A1O是三棱柱ABD－A1B1D1的高．

又AO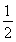＝AC＝1，AA1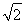＝，∴A1O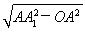＝ ＝1.

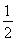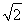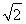又S△ABD＝××＝1，

∴V三棱柱ABD－A1B1D1＝S△ABD·A1O＝1.