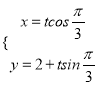题目内容
【题目】设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)<0,试判断y=f(x)的单调性并求使不等式f(x2+tx)+f(4﹣x)<0恒成立的t的取值范围;
(3)若f(1)= ![]() ,g(x)=a2x+a﹣2x﹣2f(x),求k∈N+在[1,+∞)上的最小值.
,g(x)=a2x+a﹣2x﹣2f(x),求k∈N+在[1,+∞)上的最小值.
【答案】
(1)解:∵f(x)是定义域为R的奇函数,∴f(0)=0,
∴1﹣(k﹣1)=0,∴k=2
(2)解:f(x)=ax﹣a﹣x(a>0且a≠1),
若f(1)<0,则a﹣ ![]() <0,
<0,
∵a>0且a≠1,
∴a2﹣1<0,即0<a<1
∵ax单调递减,a﹣x单调递增,
故f(x)在R上单调递减.
不等式化为f(x2+tx)<f(x﹣4),
∴x2+tx>x﹣4,即x2+(t﹣1)x+4>0恒成立
∴△=(t﹣1)2﹣16<0,解得﹣3<t<5
(3)解: ![]() ,
,
∴ ![]() ,
,
∴ ![]()
g(x)=22x+2﹣2x﹣2(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2(2x﹣2﹣x)+2
令t=2x﹣2﹣x
∵t=2x﹣2﹣x在[1,+∞)上为递增的,
∴ ![]()
∴设h(t)=t2﹣2t+2=(t﹣1)2+1, ![]()
∴ ![]() ,
,
即g(x)在[1,+∞)上的最小值为 ![]()
【解析】(1)根据函数奇偶性的定义和性质进行求解即可.(2)根据不等式求出a的取值范围,判断函数的单调性,将不等式恒成立进行转化即可.(3)利用换元法,结合一元二次函数单调性的性质进行求解即可.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目