题目内容
点P(x,y)满足(x+2)2+(y+3)2=1求:
(1)求
的最大值
(2)x-2y的最小值.
(1)求
| y+3 |
| x-2 |
(2)x-2y的最小值.
(1)设
=k,则
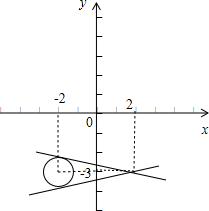
表示圆上的点与点(2,-3)连线的斜率,
由图象可知当直线
=k与圆相切时斜率达到最大值和最小值.
直线kx-y-2k-3=0与圆(x+2)2+(y+3)2=1相切时满足圆心(-2,-3)到直线的距离等于半径,
即
=1,解得k=±
,故
的最大值是
;
(2)由圆的方程可令x=-2+cosθ,y=-3+sinθ,
∴x-2y=-2+cosθ+6-2sinθ=4+
cos(θ+ϕ),
∵-1≤cos(θ+ϕ)≤1,
∴x-2y的最小值是4-
| y+3 |
| x-2 |
| y+3 |
| x-2 |
由图象可知当直线
| y+3 |
| x-2 |
直线kx-y-2k-3=0与圆(x+2)2+(y+3)2=1相切时满足圆心(-2,-3)到直线的距离等于半径,
即
| |-2k+3-2k-3| | ||
|
| ||
| 15 |
| y+3 |
| x-2 |
| ||
| 15 |
(2)由圆的方程可令x=-2+cosθ,y=-3+sinθ,
∴x-2y=-2+cosθ+6-2sinθ=4+
| 5 |
∵-1≤cos(θ+ϕ)≤1,
∴x-2y的最小值是4-
| 5 |


练习册系列答案
相关题目
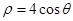 ,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是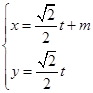 (t是参数)
(t是参数)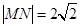 ,求实数m的值.
,求实数m的值.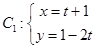 (t为参数)与曲线
(t为参数)与曲线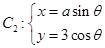 (
(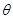 为参数,
为参数,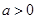 )有一个公共点在x轴上,则
)有一个公共点在x轴上,则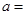 .
.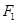 是椭圆
是椭圆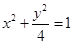 的下焦点,
的下焦点,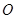 为坐标原点,点
为坐标原点,点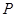 在椭圆上,则
在椭圆上,则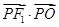 的最大值为
的最大值为 .
.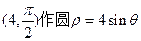 的切线,则切线的极坐标方程是 。
的切线,则切线的极坐标方程是 。