题目内容
(坐标系与参数方程选做题)在极坐标系中,直线l:ρcosθ=t(常数t>0)与曲线C:ρ=2sinθ相切,则t=______.
直线l:ρcosθ=t (常数t>0)即x=t. 曲线C:ρ=2sinθ 即 ρ2=2ρsinθ,故 x2+(y-1)2=1,
表示以(0,1)为圆心,以1为半径的圆.
再由直线l和圆相切,可得 1=t-0,解得t=1,
故答案为 1.
表示以(0,1)为圆心,以1为半径的圆.
再由直线l和圆相切,可得 1=t-0,解得t=1,
故答案为 1.

练习册系列答案
相关题目
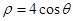 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线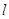 的参数方程是
的参数方程是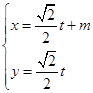 (t是参数)。若直线
(t是参数)。若直线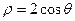 ,则该圆的圆心到直线
,则该圆的圆心到直线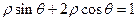 的距离是 .
的距离是 .
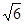 ),则它的球坐标为_______,柱坐标为______
),则它的球坐标为_______,柱坐标为______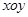 中,曲线C1的参数方程为
中,曲线C1的参数方程为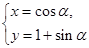 (
(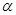 为参数)在极坐标系(与直角坐标系
为参数)在极坐标系(与直角坐标系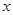 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线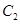 的方程为
的方程为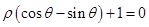 ,则
,则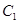 与
与