题目内容
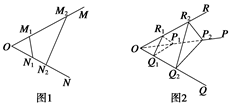
如图1,若射线OM,ON上分别存在点M1,M2与点N1,N2,则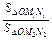 =
=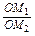 ·
·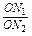 ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
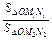 =
=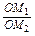 ·
·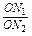 ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
类似的结论为: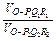 =
=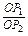 ·
·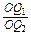 ·
·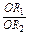 .
.
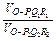 =
=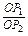 ·
·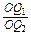 ·
·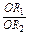 .
. 类似的结论为: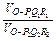 =
=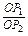 ·
·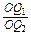 ·
·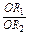 .
.
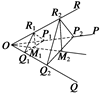
这个结论是正确的,证明如下:
如图,过R2作R2M2⊥平面P2OQ2于M2,连OM2.
过R1在平面OR2M2作R1M1∥R2M2交OM2于M1,
则R1M1⊥平面P2OQ2.
由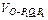 =
=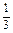
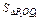 ·R1M1
·R1M1
=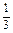 ·
·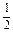 OP1·OQ1·sin∠P1OQ1·R1M1
OP1·OQ1·sin∠P1OQ1·R1M1
=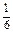 OP1·OQ1·R1M1·sin∠P1OQ1,
OP1·OQ1·R1M1·sin∠P1OQ1,
同理,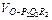 =
=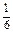 OP2·OQ2·R2M2·sin∠P2OQ2.
OP2·OQ2·R2M2·sin∠P2OQ2.
所以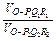 =
=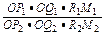 .
.
由平面几何知识可得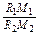 =
=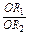 .
.
所以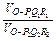 =
=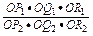 .所以结论正确.
.所以结论正确.
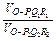 =
=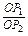 ·
·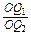 ·
·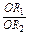 .
.
这个结论是正确的,证明如下:
如图,过R2作R2M2⊥平面P2OQ2于M2,连OM2.
过R1在平面OR2M2作R1M1∥R2M2交OM2于M1,
则R1M1⊥平面P2OQ2.
由
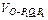 =
=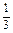
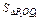 ·R1M1
·R1M1=
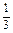 ·
·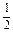 OP1·OQ1·sin∠P1OQ1·R1M1
OP1·OQ1·sin∠P1OQ1·R1M1=
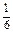 OP1·OQ1·R1M1·sin∠P1OQ1,
OP1·OQ1·R1M1·sin∠P1OQ1,同理,
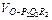 =
=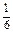 OP2·OQ2·R2M2·sin∠P2OQ2.
OP2·OQ2·R2M2·sin∠P2OQ2.所以
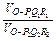 =
=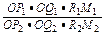 .
.由平面几何知识可得
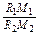 =
=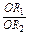 .
.所以
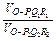 =
=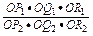 .所以结论正确.
.所以结论正确.
练习册系列答案
相关题目
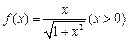 ,数列
,数列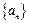 满足
满足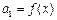 ,
,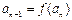 .
.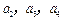 ;
;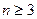 ,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数
,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数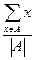 与
与 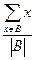
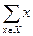 与
与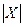 分别表示有限数集
分别表示有限数集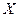 的所有元素之和及元素个数.)
的所有元素之和及元素个数.)
 ,请你写出一个具有一般性的等式,使你写出的等式包含了已知的等式(不要求证明),这个等式是_________ .
,请你写出一个具有一般性的等式,使你写出的等式包含了已知的等式(不要求证明),这个等式是_________ .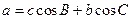 ;类比上述结论,写出下列条件下的结论:四面体P-ABC中,△ABC,△PAB,△PBC,△PCA的面积分别是
;类比上述结论,写出下列条件下的结论:四面体P-ABC中,△ABC,△PAB,△PBC,△PCA的面积分别是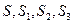 ,二面角
,二面角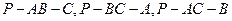 的度数分别是
的度数分别是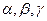 ,则
,则 ;
;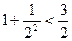 ,
, 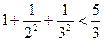 ,
, 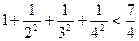 , . . . . . .
, . . . . . . …则可归纳出_________.
…则可归纳出_________. ,使得
,使得 能被
能被