题目内容
给定整数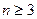 ,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数
,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数
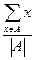 与
与 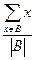
是互素的合数.(这里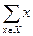 与
与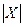 分别表示有限数集
分别表示有限数集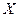 的所有元素之和及元素个数.)
的所有元素之和及元素个数.)
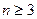 ,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数
,证明:存在n个互不相同的正整数组成的集合S,使得对S的任意两个不同的非空子集A,B,数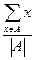 与
与 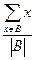
是互素的合数.(这里
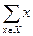 与
与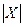 分别表示有限数集
分别表示有限数集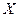 的所有元素之和及元素个数.)
的所有元素之和及元素个数.)见解析
我们用 表示有限数集X中元素的算术平均.
表示有限数集X中元素的算术平均.
第一步,我们证明,正整数的n元集合 具有下述性质:对
具有下述性质:对 的任意两个不同的非空子集A,B,有
的任意两个不同的非空子集A,B,有 .
.
证明:对任意 ,
, ,设正整数k满足
,设正整数k满足
 , ①
, ①
并设l是使 的最小正整数.我们首先证明必有
的最小正整数.我们首先证明必有 .
.
事实上,设 是A中最大的数,则由
是A中最大的数,则由 ,易知A中至多有
,易知A中至多有 个元素,即
个元素,即 ,故
,故 .又由
.又由 的定义知
的定义知

 ,故由①知
,故由①知 .特别地有
.特别地有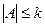 .
.
此外,显然 ,故由l的定义可知
,故由l的定义可知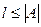 .于是我们有
.于是我们有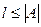
 .
.
若 ,则
,则 ;否则有
;否则有 ,则
,则


 .
.
由于 是A中最大元,故上式表明
是A中最大元,故上式表明 .结合
.结合 即知
即知 .
.
现在,若有 的两个不同的非空子集A,B,使得
的两个不同的非空子集A,B,使得 ,则由上述证明知
,则由上述证明知 ,故
,故 ,但这等式两边分别是A,B的元素和,利用
,但这等式两边分别是A,B的元素和,利用 易知必须A=B,矛盾.
易知必须A=B,矛盾.
第二步,设K是一个固定的正整数,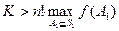 ,我们证明,对任何正整数x,正整数的n元集合
,我们证明,对任何正整数x,正整数的n元集合 具有下述性质:对
具有下述性质:对 的任意两个不同的非空子集A,B,数
的任意两个不同的非空子集A,B,数 与
与 是两个互素的整数.
是两个互素的整数.
事实上,由 的定义易知,有
的定义易知,有 的两个子集
的两个子集 ,满足
,满足 ,
, ,且
,且
 . ②
. ②
显然 及
及 都是整数,故由上式知
都是整数,故由上式知 与
与 都是正整数.
都是正整数.
现在设正整数d是 与
与 的一个公约数,则
的一个公约数,则 是d的倍数,
是d的倍数,
故由②可知 ,但由K的选取及
,但由K的选取及 的构作可知,
的构作可知, 是小于K的非零整数,故它是
是小于K的非零整数,故它是 的约数,从而
的约数,从而 .再结合
.再结合 及②可知d=1,故
及②可知d=1,故 与
与 互素.
互素.
第三步,我们证明,可选择正整数x,使得 中的数都是合数.由于素数有无穷多个,
中的数都是合数.由于素数有无穷多个,
故可选择n个互不相同且均大于K的素数 .将
.将 中元素记为
中元素记为 ,
,
则 ,且
,且 (对
(对 ),
),
故由中国剩余定理可知,同余方程组
 ,
,
有正整数解.
任取这样一个解x,则相应的集合 中每一项显然都是合数.结合第二步的结果,这一n元集合满足问题的全部要求.
中每一项显然都是合数.结合第二步的结果,这一n元集合满足问题的全部要求.
 表示有限数集X中元素的算术平均.
表示有限数集X中元素的算术平均.第一步,我们证明,正整数的n元集合
 具有下述性质:对
具有下述性质:对 的任意两个不同的非空子集A,B,有
的任意两个不同的非空子集A,B,有 .
.证明:对任意
 ,
, ,设正整数k满足
,设正整数k满足 , ①
, ①并设l是使
 的最小正整数.我们首先证明必有
的最小正整数.我们首先证明必有 .
.事实上,设
 是A中最大的数,则由
是A中最大的数,则由 ,易知A中至多有
,易知A中至多有 个元素,即
个元素,即 ,故
,故 .又由
.又由 的定义知
的定义知

 ,故由①知
,故由①知 .特别地有
.特别地有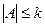 .
.此外,显然
 ,故由l的定义可知
,故由l的定义可知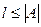 .于是我们有
.于是我们有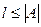
 .
.若
 ,则
,则 ;否则有
;否则有 ,则
,则

 .
.由于
 是A中最大元,故上式表明
是A中最大元,故上式表明 .结合
.结合 即知
即知 .
.现在,若有
 的两个不同的非空子集A,B,使得
的两个不同的非空子集A,B,使得 ,则由上述证明知
,则由上述证明知 ,故
,故 ,但这等式两边分别是A,B的元素和,利用
,但这等式两边分别是A,B的元素和,利用 易知必须A=B,矛盾.
易知必须A=B,矛盾.第二步,设K是一个固定的正整数,
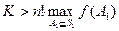 ,我们证明,对任何正整数x,正整数的n元集合
,我们证明,对任何正整数x,正整数的n元集合 具有下述性质:对
具有下述性质:对 的任意两个不同的非空子集A,B,数
的任意两个不同的非空子集A,B,数 与
与 是两个互素的整数.
是两个互素的整数.事实上,由
 的定义易知,有
的定义易知,有 的两个子集
的两个子集 ,满足
,满足 ,
, ,且
,且 . ②
. ②显然
 及
及 都是整数,故由上式知
都是整数,故由上式知 与
与 都是正整数.
都是正整数.现在设正整数d是
 与
与 的一个公约数,则
的一个公约数,则 是d的倍数,
是d的倍数,故由②可知
 ,但由K的选取及
,但由K的选取及 的构作可知,
的构作可知, 是小于K的非零整数,故它是
是小于K的非零整数,故它是 的约数,从而
的约数,从而 .再结合
.再结合 及②可知d=1,故
及②可知d=1,故 与
与 互素.
互素.第三步,我们证明,可选择正整数x,使得
 中的数都是合数.由于素数有无穷多个,
中的数都是合数.由于素数有无穷多个,故可选择n个互不相同且均大于K的素数
 .将
.将 中元素记为
中元素记为 ,
,则
 ,且
,且 (对
(对 ),
),故由中国剩余定理可知,同余方程组
 ,
,有正整数解.
任取这样一个解x,则相应的集合
 中每一项显然都是合数.结合第二步的结果,这一n元集合满足问题的全部要求.
中每一项显然都是合数.结合第二步的结果,这一n元集合满足问题的全部要求.
练习册系列答案
相关题目
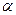 、
、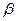 (如图1),则
(如图1),则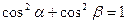 .用类比的方法,把它推广到空间长方体中,试写出相应的一个真命题并证明。
.用类比的方法,把它推广到空间长方体中,试写出相应的一个真命题并证明。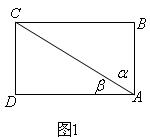
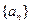 中,
中,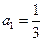 ,且前n项的算术平均数等于第n项的2n-1倍(
,且前n项的算术平均数等于第n项的2n-1倍(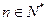 )。
)。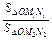 =
=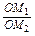 ·
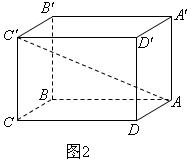
·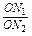 ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?这个结论正确吗?说明理由.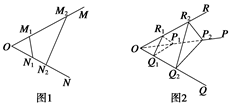
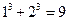 ; ⑵
; ⑵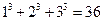 ;⑵
;⑵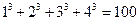 ,
, .
. 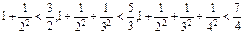 ,…,则可归纳出式子为( )
,…,则可归纳出式子为( )




 13.
13.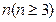 维向量,
维向量,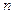 维向量可用
维向量可用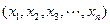 表示.设
表示.设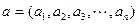 ,
,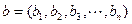 ,规定向量
,规定向量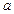 与
与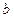 夹角
夹角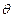 的余弦为
的余弦为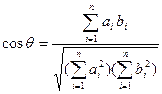 .当
.当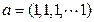 ,
,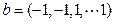 时,
时,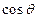 =" "
=" "  B.
B. C.
C. D.
D.