题目内容
【题目】选修4—4：坐标系与参数方程．
已知直线l的参数方程为
(t为参数)，曲线C的极坐标方程为： 
(1)求直线l的倾斜角和曲线C的直角坐标方程；
(2)设直线l与曲线C交于A，B两点，求|AB|.
【答案】（1）曲线C的直角坐标方程为
；（2）
【解析】试题分析: (1)直线
的参数方程为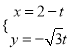
(t为参数)，消去参数
化为普通方程可得，进而得到倾斜角．曲线
的极坐标方程为
，即
利用
，即可化为直角坐标方程．
（2）直线方程与双曲线方程联立化为
，利用
即可得出．
试题解析：(1)直线l的普通方程为
x－y－2
＝0，
∴其斜率为
，
∴直线l的倾斜角为
.
∵曲线C的极坐标方程为1－3sin2θ＝
，即ρ2－3ρ2sin2θ＝2，
∴曲线C的直角坐标方程为x2－2y2＝2.
(2)可得直线l的参数方程的标准形式为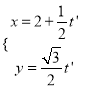
(t′为参数)，代入曲线C的直角坐标方程x2－2y2＝2得
∴
.
练习册系列答案
相关题目
【题目】某单位有车牌尾号为
的汽车
和尾号为
的汽车
，两车分属于两个独立业务部分．对一段时间内两辆汽车的用车记录进行统计，在非限行日， 
车日出车频率
， 
车日出车频率
．该地区汽车限行规定如下：
车尾号 |
|
|
|
|
|
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
现将汽车日出车频率理解为日出车概率，且
， 
两车出车相互独立．
（I）求该单位在星期一恰好出车一台的概率．
（II）设
表示该单位在星期一与星期二两天的出车台数之和，求
的分布列及其数学期望
．
