题目内容
【题目】已知函数f(x)的定义域为(0,+∞),f(2)=1,f(xy)=f(x)+f(y)且当x>1时,f(x)>0.
(1)判断函数f(x)在其定义域(0,+∞)上的单调性并证明;
(2)解不等式f(x)+f(x﹣2)≤3.
【答案】
(1)解:函数f(x)在定义域(0,+∞)上单调递增.
证明如下:
设0<x1<x2,则 ![]() >1,
>1,
∵当x>1时,f(x)>0恒成立,f(x)+f( ![]() )=0,
)=0,
∴f(x2)﹣f(x1)=f(x2)+f( ![]() )=f(
)=f( ![]() )>0,
)>0,
∴f(x1)<f(x2),
∴函数f(x)在定义域(0,+∞)上单调递增
(2)解:∵f(x)+f(x﹣2)≤3=f(8),且函数f(x)在定义域(0,+∞)上单调递增,
∴ 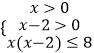 ,解得:2<x≤4,
,解得:2<x≤4,
∴不等式f(x)+f(x﹣2)≤3的解集为{x|2<x≤4}
【解析】(1)设0<x1<x2 ![]() >1,依题意,利用单调性的定义可证得,函数f(x)在定义域(0,+∞)上单调递增;(2)f(x)+f(x﹣2)≤3f(x)+f(x﹣2)≤f(8)
>1,依题意,利用单调性的定义可证得,函数f(x)在定义域(0,+∞)上单调递增;(2)f(x)+f(x﹣2)≤3f(x)+f(x﹣2)≤f(8) 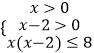 ,解之即可.
,解之即可.

练习册系列答案
相关题目