题目内容
【题目】已知函数![]() (
(![]() 为常数).
为常数).
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,设
时,设![]() 的两个极值点
的两个极值点![]() ,
,![]() (
(![]() )恰为
)恰为![]() 的零点,求
的零点,求![]() 的最小值.
的最小值.
【答案】(1)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() .(2)
.(2)![]()
【解析】
试题分析:(1)首先求函数的导数![]() ,分
,分![]() 三种情况解
三种情况解![]() 或
或![]() 的解集,得到函数的单调区间;(2)首先求
的解集,得到函数的单调区间;(2)首先求![]() ,得到
,得到![]() ,根据
,根据![]() ,得到
,得到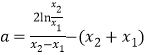 ,代入
,代入![]() 并化简为
并化简为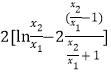 ,根据前面根与系数的关系和
,根据前面根与系数的关系和![]() 的取值范围,得到
的取值范围,得到![]() 的取值范围,通过设
的取值范围,通过设![]() 转化为关于
转化为关于![]() 的函数求最小值.
的函数求最小值.
试题解析:(1)![]() ,
,![]() ,
,
当![]() 时,由
时,由![]() ,解得
,解得![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() 单调递增;由
单调递增;由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,故
,故![]() ,即
,即![]() 在
在![]() 上单调递增.
上单调递增.
所以当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)由![]() 得
得![]() ,
,
由已知![]() 有两个互异实根
有两个互异实根![]() ,
,![]() ,
,
由根与系数的关系得![]() ,
,![]() ,
,
因为![]() ,
,![]() (
(![]() )是
)是![]() 的两个零点,故
的两个零点,故![]() ①
①
![]() ②
②
由②![]() ①得:
①得:![]() ,
,
解得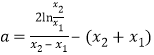 ,
,
因为![]() ,得
,得![]() ,
,
将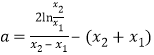 代入得
代入得
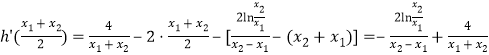
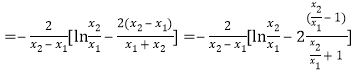 ,
,
所以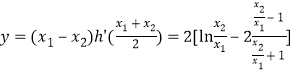 ,
,
设![]() ,因为
,因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
构造![]() ,得
,得![]() ,
,
则![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,即
,即![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
