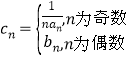题目内容
【题目】
已知公比为整数的正项等比数列
满足： 
， 
．
（1）求数列的通项公式；
（2）令
，求数列
的前
项和
．
【答案】(1) 
.
(2) 
.
【解析】试题分析：第一问根据等比数列的通项公式以及性质，结合题的条件，转化为关于首项和公比的等量关系式，从而求得结果；第二问利用错位相减法求和，从而求得结果.
（1）设等比数列
的公比为
，
由
，有
可得
，…………………1分
由
可得
，…………………2分
两式相除可得： 
，…………………3分
整理为： 
，
由
，且为整数，可解得
，故
…………………5分
数列的通项公式为．…………………7分
（2）由
，
，
有
，…………………9分
两式作差有： 
，…………………11分
得
，…………………14分
故
．…………………15分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】已知函数
的一系列对应值如下表：
|
|
|
|
|
|
|
|
| -1 | 1 | 3 | 1 | -1 | 1 | 3 |
（1）根据表格提供的数据画出函数
的图像并求出函数解析式；
（2）根据(1)的结果，若函数
的周期为
，当
时，方程
恰有两个不同的解，求实数
的取值范围．
