题目内容
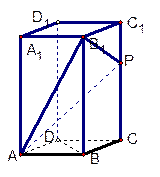
如图,在长方体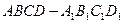 中,
中,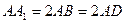 ,且
,且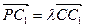
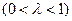 .
.
(Ⅰ)求证:对任意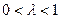 ,总有
,总有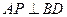 ;
;
(Ⅱ)若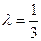 ,求二
,求二 面角
面角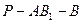 的余弦值;
的余弦值;
(Ⅲ)是否存在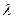 ,使得
,使得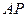 在平面
在平面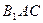 上的射影平分
上的射影平分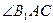 ?若存在,求出
?若存在,求出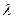 的值,若不存在,说明理由.
的值,若不存在,说明理由.
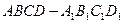 中,
中,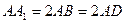 ,且
,且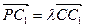
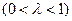 .
.
(Ⅰ)求证:对任意
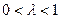 ,总有
,总有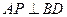 ;
;(Ⅱ)若
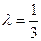 ,求二
,求二 面角
面角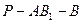 的余弦值;
的余弦值;(Ⅲ)是否存在
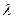 ,使得
,使得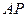 在平面
在平面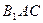 上的射影平分
上的射影平分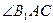 ?若存在,求出
?若存在,求出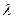 的值,若不存在,说明理由.
的值,若不存在,说明理由.(Ⅰ)证明略
(Ⅱ)
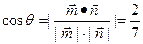
(Ⅲ)
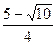
解:(Ⅰ)如图,以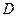 为坐标原点,分别以
为坐标原点,分别以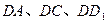
所在直线为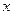 轴,
轴,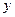 轴,
轴,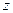 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
不妨设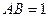 .
.
则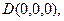
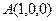 ,
,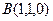 ,
,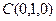 ,
,
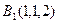 ,
,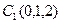 ,
,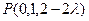 ,
,
从而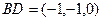 ,
,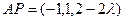 ,
,
所以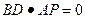 ,即
,即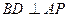 ;能 -----------------4分
;能 -----------------4分
(Ⅱ)由(Ⅰ)及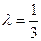 得,
得,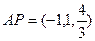 ,
,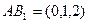
设平面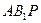 的法向量为
的法向量为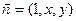 ,则
,则
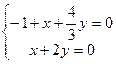 ,解方程组得
,解方程组得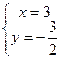 ,
,
从而可取平面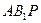 的法向量为
的法向量为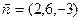 ,
,
又取平面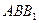 的法向量为
的法向量为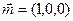 ,且设二面角P-AB1-B为
,且设二面角P-AB1-B为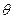 ,
,
所以
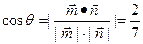 ; ----------------------------
; ---------------------------- ----------------9分
----------------9分
(Ⅲ)假设存在实数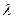
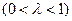 满足条件,由题结合图形,只需满足向量
满足条件,由题结合图形,只需满足向量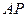 分别与向量
分别与向量 的所成角相同,即有
的所成角相同,即有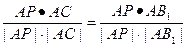 ,
,
即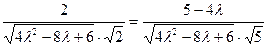 ,解得
,解得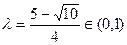 ,所以存在满足题意的实数
,所以存在满足题意的实数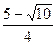 ,使得
,使得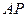 在平面
在平面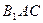 上的射影平分
上的射影平分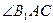 .--------14分
.--------14分
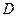 为坐标原点,分别以
为坐标原点,分别以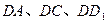
所在直线为
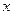 轴,
轴,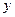 轴,
轴,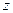 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,不妨设
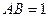 .
.则
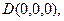
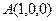 ,
,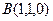 ,
,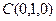 ,
,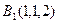 ,
,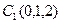 ,
,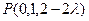 ,
,从而
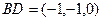 ,
,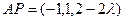 ,
,所以
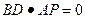 ,即
,即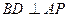 ;能 -----------------4分
;能 -----------------4分(Ⅱ)由(Ⅰ)及
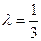 得,
得,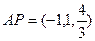 ,
,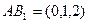
设平面
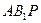 的法向量为
的法向量为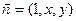 ,则
,则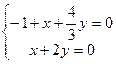 ,解方程组得
,解方程组得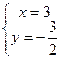 ,
,从而可取平面
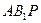 的法向量为
的法向量为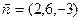 ,
,又取平面
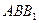 的法向量为
的法向量为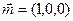 ,且设二面角P-AB1-B为
,且设二面角P-AB1-B为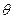 ,
,所以

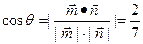 ; ----------------------------
; ---------------------------- ----------------9分
----------------9分(Ⅲ)假设存在实数
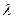
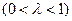 满足条件,由题结合图形,只需满足向量
满足条件,由题结合图形,只需满足向量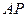 分别与向量
分别与向量 的所成角相同,即有
的所成角相同,即有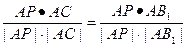 ,
,即
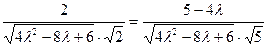 ,解得
,解得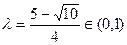 ,所以存在满足题意的实数
,所以存在满足题意的实数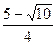 ,使得
,使得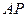 在平面
在平面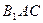 上的射影平分
上的射影平分 .--------14分
.--------14分
练习册系列答案
相关题目
 ,BC=4,
,BC=4,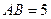 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.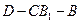 的余弦值.
的余弦值.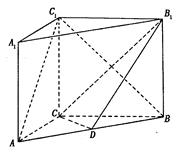


 的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA
的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA 1C1C,且A1B=AB=AC=1.
1C1C,且A1B=AB=AC=1.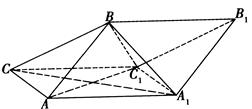
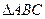 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边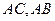 上分别取点
上分别取点 ,使得
,使得 ,把
,把 沿直线
沿直线 折起,使
折起,使 =90°,得四棱锥
=90°,得四棱锥 (如图2).在四棱锥
(如图2).在四棱锥
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  时,试在
时,试在 上确定一点G,使得
上确定一点G,使得 ,并证明你的结论.
,并证明你的结论.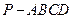 中,
中,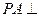 底面
底面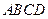 ,
,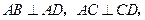
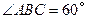 ,
,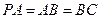 ,
,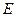 是
是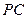 的中点.
的中点.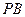 和平面
和平面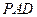 所成的角的大小;
所成的角的大小;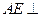 平面
平面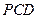 ;
;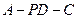 的正弦值
的正弦值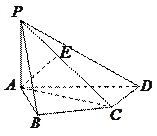
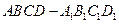 的底面
的底面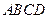 是菱形,
是菱形,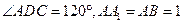 ,点
,点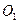 、
、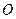 分别是上、下底面菱形的对角线的交点.⑴求证:
分别是上、下底面菱形的对角线的交点.⑴求证: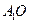 ∥平面
∥平面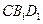 ;⑵求点
;⑵求点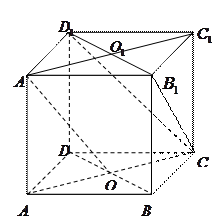
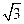 ,
,