题目内容
【题目】几位大学生响应国家的创业号召，开发了一款应用软件，为激发大家的学习兴趣，他们推出了“解数学题获取软件激活码”的活动，这款软件的激活码为下列数学问题的答案：已知数列1、1、2、1、2、4、8、1、2、4、8、16、……，其中第一项是
，接下来的两项是
，再接下来的三项是
，……，以此类推，求满足如下条件的最小整数
且该数列的前
项和为2的整数幂，那么该软件的激活码是________。
【答案】
【解析】
由题意先将此数列分组，再求得前
组的项之和为
及项数，由题意可知
为2的整数幂，只需将
消去即可，再分别讨论即可得解.
解：由题意可知，将1、1、2、1、2、4、8、1、2、4、8、16、……，可分为
，
，
，
，
，
根据等比数列前项和公式，求得每组和分别为
，
，
，
，
，
每组含有的项数为：
，总共的项数为
，
所有组的项之和为
，由题意可知：为2的整数幂，只需将消去即可，
则①
，解得
，总共有
项，不满足
，
②
，解得
，总共有
项，不满足，
③
，解得
，总共有
项，不满足，
④
，解得
，总共有
项，满足，
即该软件的激活码是，
故答案为：.
【题目】辽宁省六校协作体（葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中）中的某校理科实验班的100名学生期中考试的语文、数学成绩都不低于100分，其中语文成绩的频率分布直方图如图所示，成绩分组区间是：[100,110），[110,120），[120,130），[130,140），[140,150]．
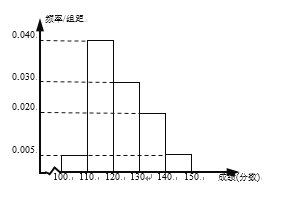
这100名学生语文成绩某些分数段的人数
与数学成绩相应分数段的人数
之比如下表所示：
分组区间 | [100,110） | [110,120） | [120,130） | [130,140） |
| 1:2 | 2:1 | 3:4 | 1:1 |
（1）估计这100名学生语文成绩的平均数、方差（同一组数据用该区间的中点值作代表）；
（2）从数学成绩在[130，150] 的学生中随机选取2人，该2人中数学成绩在[140，150]的人数为
，求的数学期望
．
