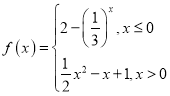Question

【题目】已知抛物线x2=4y．

（1）求抛物线在点P（2，1）处的切线方程；

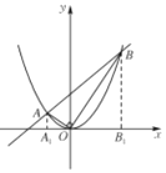
（2）若不过原点的直线l与抛物线交于A，B两点（如图所示），且OA⊥OB，|OA|=|OB|，求直线l的斜率．

Answer 1

【答案】（1）y=x-1; （2）

【解析】

（1）方法一，利用导数的几何意义即可求出切线方程； 方法二，利用判别式即可求出切线方程；

（2）设直线l方程以及AB两点坐标，根据根与系数的关系，以及相似三角形即可求出．

解：（1）方法一：点P（2，1）在抛物线上，即y=x2，

∴y′=x，

∴切线的斜率k=y′|=×2=1，

∴抛物线在点P（2，1）处的切线方程为y=x-1，

方法二：设抛物线在点P（2，1）处的切线方程为y-1=k（x-2），（k＞0），即y=kx+1-2k，

代入到x2=4y，可得x2-4kx+8k-4=0，

由△=16k2-4（8k-4）=0，

解得k=1，

∴抛物线在点P（2，1）处的切线方程为y=x-1，

（2）设直线l方程为：y=kx+m，（k＞0，m＞0），A（x1，y1），B（x2，y2），

由，消去y得x2-4kx-4m=0，

∴x1+x2=4k，x1x2=-4m，

∵OA⊥OB，

∴=0，

∴x1x2+y1y2=0，

∴x1x2+=0，

解得x1x2=-16，或x1x2=0（舍去）

∴-4m=-16，

∴m=4，

过点A，B两点分别作x轴的垂线，垂足为A1，B1，

∵OA⊥OB，

∴∠AOB=90°，

∵∠AOB+∠AOA1+∠BOB1=180°，

∴∠AOA1+∠BOB1=90°，

∵∠OBB1+∠BOB1=90°，

∴∠AOA1=∠OBB1，

∴Rt△AA1O∽Rt△OB1B，

∴==，

∴y2=-8x1，x22=-32x1，

∵x1x2=-16，

∴x1=-2，x2=8，

∴x1+x2=6=4k，

解得k=，

∴直线l的斜率为．