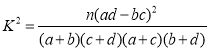题目内容
【题目】已知抛物线![]() 的顶点在坐标原点,其焦点
的顶点在坐标原点,其焦点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 为直线
为直线![]() 上一点,圆
上一点,圆![]() 与
与![]() 轴相切(
轴相切(![]() 为圆心),且
为圆心),且![]() ,
,![]() 关于点
关于点![]() 对称.
对称.
(1)求圆![]() 和抛物线
和抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,交抛物线
两点,交抛物线![]() 于
于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
【答案】(1)![]() 的标准方程为
的标准方程为![]() .
.![]() 的标准方程为
的标准方程为![]() (2)见证明
(2)见证明
【解析】
(1)根据题意可得 ,解得a、p,即可求出圆与抛物线的标准方程,
,解得a、p,即可求出圆与抛物线的标准方程,
(2)设l的斜率为k,那么其方程为y=k(x+2),根据韦达定理和弦长公式即可证明.
(1)设抛物线![]() 的标准方程为
的标准方程为![]() ,则焦点
,则焦点![]() 的坐标为
的坐标为![]() .
.
已知![]() 在直线
在直线![]() 上,故可设
上,故可设![]()
因为![]() ,
,![]() 关于
关于![]() 对称,所以
对称,所以 ,解得
,解得![]()
所以![]() 的标准方程为
的标准方程为![]() .
.
因为![]() 与
与![]() 轴相切,故半径
轴相切,故半径![]() ,
,
所以![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1)知,直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,且方程为
,且方程为![]()
则![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,![]()
由![]() 消去
消去![]() 并整理得:
并整理得:![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
所以![]()
![]()
![]()
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]()
所以![]() ,即
,即![]() .
.

【题目】已知![]() 元集合
元集合![]() 的一些子集满足:每个子集至少含2个元素,每两个不同子集的交集至多含2个元素,记这些子集的元素个数的立方和为
的一些子集满足:每个子集至少含2个元素,每两个不同子集的交集至多含2个元素,记这些子集的元素个数的立方和为![]() .问:是否存在不小于3的正整数
.问:是否存在不小于3的正整数![]() ,使
,使![]() 的最大值等于2009的方幂?说明你的理由.
的最大值等于2009的方幂?说明你的理由.
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期低于平均数的患者,称为“短潜伏者”,潜伏期不低于平均数的患者,称为“长潜伏者”.
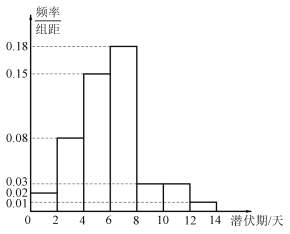
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |