题目内容
设角A,B,C为△ABC的三个内角.
(1)设f(A)=sin A+2sin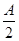 ,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
(2)当A取A0时,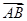 ·
·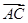 =-1,求BC边长的最小值.
=-1,求BC边长的最小值.
(1)设f(A)=sin A+2sin
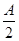 ,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;(2)当A取A0时,
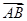 ·
·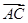 =-1,求BC边长的最小值.
=-1,求BC边长的最小值.(1)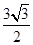 (2)
(2)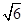
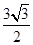 (2)
(2)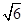
(1)f′(A)=cos A+cos 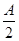 =2cos2
=2cos2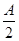 +cos
+cos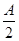 -1=
-1=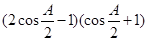 .
.
因为0<A<π,所以cos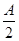 +1>0.由f′(A)>0,得cos
+1>0.由f′(A)>0,得cos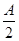 >
>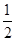 ,所以0<
,所以0<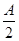 <
<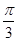 ,即0<A<
,即0<A<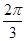 .所以当A∈
.所以当A∈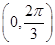 时,f(A)为增函数;当A∈
时,f(A)为增函数;当A∈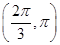 时,f(A)为减函数.故A0=
时,f(A)为减函数.故A0=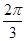 时,f(A)取极大值f(A0)=f
时,f(A)取极大值f(A0)=f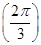 =
=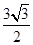 .
.
(2)设a,b,c是角A,B,C的对边.由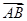 ·
·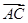 =-1知bc=2,而a=
=-1知bc=2,而a=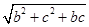 ≥
≥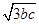 =
=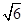
当且仅当b=c=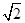 时,BC边长的最小值为
时,BC边长的最小值为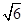 .
.
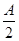 =2cos2
=2cos2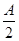 +cos
+cos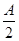 -1=
-1=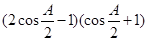 .
.因为0<A<π,所以cos
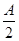 +1>0.由f′(A)>0,得cos
+1>0.由f′(A)>0,得cos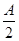 >
>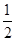 ,所以0<
,所以0<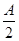 <
<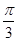 ,即0<A<
,即0<A<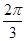 .所以当A∈
.所以当A∈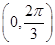 时,f(A)为增函数;当A∈
时,f(A)为增函数;当A∈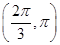 时,f(A)为减函数.故A0=
时,f(A)为减函数.故A0=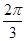 时,f(A)取极大值f(A0)=f
时,f(A)取极大值f(A0)=f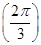 =
=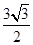 .
.(2)设a,b,c是角A,B,C的对边.由
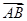 ·
·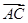 =-1知bc=2,而a=
=-1知bc=2,而a=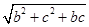 ≥
≥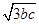 =
=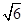
当且仅当b=c=
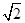 时,BC边长的最小值为
时,BC边长的最小值为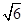 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,角A,B,C所对边分别为a,b,c,且向量
中,角A,B,C所对边分别为a,b,c,且向量 ,
, ,满足
,满足
 成等差数列,且
成等差数列,且 ,求边
,求边 的长
的长 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记 ,
,
 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大? 、
、 是两个小区所在地,
是两个小区所在地, 的垂直距离分别为
的垂直距离分别为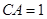
 ,
,

 ,在
,在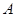 、
、 、
、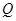 ,在
,在 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得
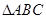 中,若
中,若 ,则
,则
 b,且a>b,则∠B等于( )
b,且a>b,则∠B等于( )
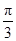




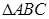 的内角
的内角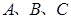 的对边分别为
的对边分别为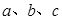 ,若
,若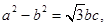
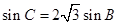 ,则
,则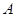 =______.
=______.