题目内容
【题目】已知直线![]() 经过点
经过点![]() .
.
(1)若原点到直线![]() 的距离为2,求直线
的距离为2,求直线![]() 的方程;
的方程;
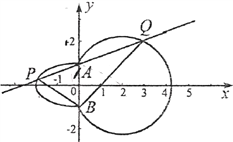
(2)若直线![]() 被两条相交直线
被两条相交直线![]() 和
和![]() 所截得的线段恰被点
所截得的线段恰被点![]() 平分,求直线
平分,求直线![]() 的方程.
的方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)本题首先可以假设直线![]() 的斜率不存在,然后根据点
的斜率不存在,然后根据点![]() 得出直线方程,再然后假设直线斜率存在并设出直线方程
得出直线方程,再然后假设直线斜率存在并设出直线方程![]() ,最后根据原点到直线
,最后根据原点到直线![]() 的距离为2即可得出结果;
的距离为2即可得出结果;
(2)本题首先可以设出直线![]() 与直线
与直线![]() ,
,![]() 的交点坐标
的交点坐标![]() 、
、![]() 分别为
分别为![]() 、
、![]() ,然后根据中点坐标的相关性质得出
,然后根据中点坐标的相关性质得出![]() 、
、![]() ,再然后根据
,再然后根据![]() 在
在![]() 上以及
上以及![]() 在
在![]() 上得出
上得出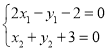 并解得
并解得![]() 的坐标是
的坐标是![]() ,最后根据直线的两点式方程即可得出结果.
,最后根据直线的两点式方程即可得出结果.
(1)①直线![]() 的斜率不存在时,显然成立,直线方程为
的斜率不存在时,显然成立,直线方程为![]() .
.
②当直线斜率存在时,设直线方程为![]() ,
,
由原点到直线![]() 的距离为2得
的距离为2得![]() ,解得
,解得![]() ,
,
故直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
综上,所求直线方程为![]() 或
或![]() .
.
(2)设直线![]() 夹在直线
夹在直线![]() ,
,![]() 之间的线段为
之间的线段为![]() (
(![]() 在
在![]() 上,
上,![]() 在
在![]() 上),
上),
![]() 、
、![]() 的坐标分别设为
的坐标分别设为![]() 、
、![]() ,
,
因为![]() 被点
被点![]() 平分,所以
平分,所以![]() ,
,![]() ,
,
于是![]() ,
,![]()
由于![]() 在
在![]() 上,
上,![]() 在
在![]() 上,即
上,即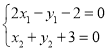 ,解得
,解得![]() ,
,![]() ,
,
即![]() 的坐标是
的坐标是![]() ,故直线
,故直线![]() 的方程是
的方程是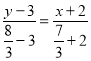 ,即
,即![]() .
.

练习册系列答案
相关题目
【题目】某高中在校学生2000人![]() 为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动
为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动![]() 每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
高一年级 | 高二年级 | 高三年级 | |
跑步 | a | b | c |
登山 | x | y | z |
其中a:b:![]() :3:5,全校参与登山的人数占总人数的
:3:5,全校参与登山的人数占总人数的![]() ,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取
,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取![]()
![]()
A. 6人B. 12人C. 18人D. 24人