题目内容
已知函数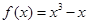 .
.
(1)求曲线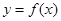 在点
在点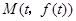 处的切线方程;
处的切线方程;
(2)设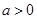 ,如果过点
,如果过点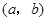 可作曲线
可作曲线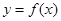 的三条切线,证明:
的三条切线,证明: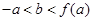
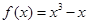 .
.(1)求曲线
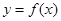 在点
在点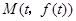 处的切线方程;
处的切线方程;(2)设
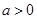 ,如果过点
,如果过点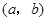 可作曲线
可作曲线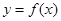 的三条切线,证明:
的三条切线,证明: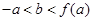
(1)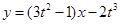 (2)设切线
(2)设切线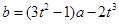 ,方程
,方程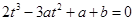 有三个相异的实数根.函数
有三个相异的实数根.函数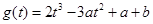 与x轴有三个交点,
与x轴有三个交点,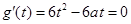 得
得
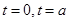 ,满足极大值
,满足极大值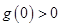 ,极小值
,极小值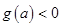 得
得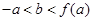
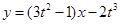 (2)设切线
(2)设切线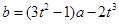 ,方程
,方程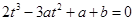 有三个相异的实数根.函数
有三个相异的实数根.函数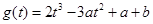 与x轴有三个交点,
与x轴有三个交点,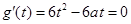 得
得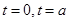 ,满足极大值
,满足极大值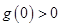 ,极小值
,极小值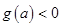 得
得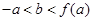
试题分析:(1)求函数
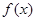 的导数;
的导数;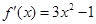 .(1分) 曲线
.(1分) 曲线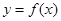 在点
在点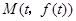 处的切线方程为:
处的切线方程为: 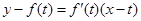 , (2分)
, (2分)即
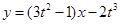 . (4分)
. (4分)(2)如果有一条切线过点
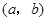 ,则存在
,则存在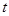 ,使
,使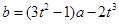 . (5分)
. (5分)于是,若过点
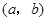 可作曲线
可作曲线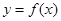 的三条切线,则方程
的三条切线,则方程 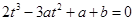 有三个相异的实数根.(6分) 记
有三个相异的实数根.(6分) 记 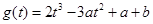 ,则
,则 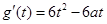
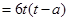 . ((7分)
. ((7分)当
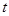 变化时,
变化时,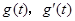 变化情况如下表:
变化情况如下表: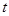 | 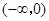 | 0 | 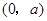 | 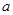 | 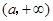 |
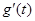 | 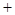 | 0 | 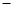 | 0 | 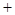 |
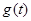 | 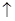 | 极大值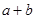 |  | 极小值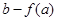 | 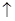 |
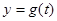 草图11分)由
草图11分)由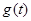 的单调性,当极大值
的单调性,当极大值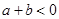 或极小值
或极小值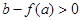 时,方程
时,方程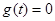 最多有一个实数根;
最多有一个实数根;当
 时,解方程
时,解方程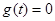 得
得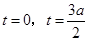 ,即方程
,即方程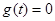 只有两个相异的实数根;
只有两个相异的实数根;当
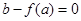 时,解方程
时,解方程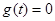 得
得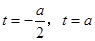 ,即方程
,即方程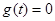 只有两个相异的实数根.
只有两个相异的实数根.综上,如果过
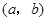 可作曲线
可作曲线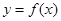 三条切线,即
三条切线,即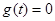 有三个相异的实数根,则
有三个相异的实数根,则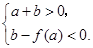 (13分) 即
(13分) 即 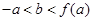 . (14分)
. (14分) 点评:几何意义:函数在某一点处的导数值等于该点处的切线斜率,第一问利用几何意义求得斜率;第二问有三条切线即有三个切点,转化为方程有三个不同的根,利用函数与方程的关系转化为函数图像与x轴有三个交点,即可通过极值判定,本题难度较大

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
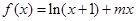 ,当
,当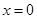 时,函数
时,函数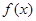 取得极大值.
取得极大值.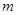 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数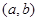 内导数都存在,且
内导数都存在,且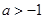 ,则存在
,则存在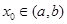 ,使得
,使得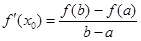 .试用这个结论证明:若
.试用这个结论证明:若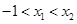 ,函数
,函数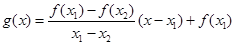 ,则对任意
,则对任意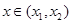 ,都有
,都有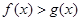 ;(Ⅲ)已知正数
;(Ⅲ)已知正数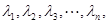 满足
满足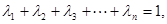 求证:当
求证:当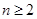 ,
,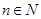 时,对任意大于
时,对任意大于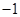 ,且互不相等的实数
,且互不相等的实数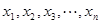 ,都有
,都有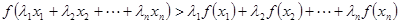
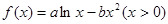 。(Ⅰ)若函数
。(Ⅰ)若函数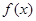 在
在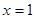 处与直线
处与直线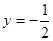 相切,①求实数
相切,①求实数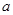 ,b的值;②求函数
,b的值;②求函数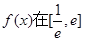 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当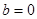 时,若不等式
时,若不等式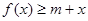 对所有的
对所有的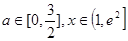 都成立,求实数m的取值范围。
都成立,求实数m的取值范围。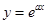 在点
在点 处的切线与直线
处的切线与直线 垂直,则
垂直,则 .
.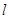 ,则f(2)+f'(2)=
,则f(2)+f'(2)= 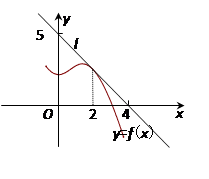
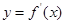 的图象,则下列命题错误的是( )
的图象,则下列命题错误的是( )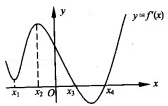
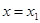 处有极小值
处有极小值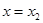 处有极大值
处有极大值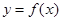 在
在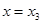 处有极小值
处有极小值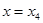 处有极小值
处有极小值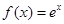 ,其图像在点
,其图像在点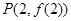 处的切线为
处的切线为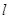 .
.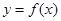 、直线
、直线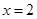 及两坐标轴围成的图形绕
及两坐标轴围成的图形绕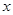 轴旋转一周所得几何体的体积;
轴旋转一周所得几何体的体积;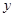 轴围成图形的面积.
轴围成图形的面积.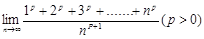 表示成定积分( )
表示成定积分( )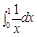
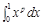
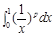
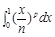
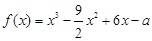 .
.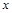 ,
,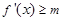 在
在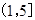 恒成立(其中
恒成立(其中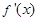 表示
表示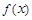 的导函数),求
的导函数),求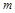 的最大值;
的最大值;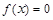 在
在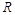 上有且仅有一个实根,求
上有且仅有一个实根,求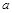 的取值范围.
的取值范围.