题目内容
设直线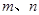 和平面
和平面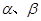 ,下列四个命题中,正确的是( )
,下列四个命题中,正确的是( )
A.若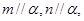 则 则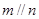 | B.若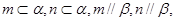 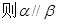 |
C.若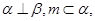 则 则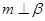 | D.若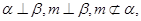 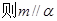 |
D
解析试题分析:对于A. 若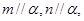 ,平行与同一个平面的两条直线的位置关系有三种,因此错误。
,平行与同一个平面的两条直线的位置关系有三种,因此错误。
对于B. 若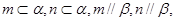
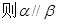 ,只有mn是相交直线的时候,符合面面平行的判定定理。故错误。
,只有mn是相交直线的时候,符合面面平行的判定定理。故错误。
对于C. 若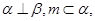 则
则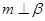 ,当两个平面垂直的时候,那么其中一个平面内任何一条直线与该平面平行,相交。不一定垂直,故错误。
,当两个平面垂直的时候,那么其中一个平面内任何一条直线与该平面平行,相交。不一定垂直,故错误。
对于D. 若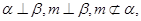
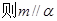 ,根据线面平行 的判定定理得到,成立,故选D.
,根据线面平行 的判定定理得到,成立,故选D.
考点:本试题考查了空间的点线面的位置关系的运用。
点评:解决该试题的关键是利用空间中的线面的平行和垂直关系的判定和性质定理,以及面面平行的位置关系的判定的运用,属于基础题。

练习册系列答案
相关题目
下列命题中,正确的是( )
| A.经过两条相交直线,有且只有一个平面 |
| B.经过一条直线和一点,有且只有一个平面 |
| C.若平面α与平面β相交,则它们只有有限个公共点 |
| D.若两个平面有三个公共点,则这两个平面重合 |
如图,在长方体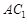 中,
中, ,
,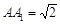 ,
,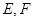 分别是面
分别是面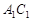 ,面
,面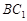 的中心,则
的中心,则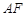 和
和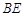 所成的角为( )
所成的角为( )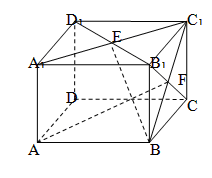
A.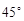 | B.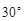 | C.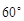 | D.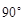 |
已知两个不同的平面α, 和两条不重合的直线m,n,则下列四种说法正确的为( )
和两条不重合的直线m,n,则下列四种说法正确的为( )
A.若m∥n,n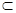 α,则m∥α α,则m∥α |
| B.若m⊥n,m⊥α,则n∥α |
C.若m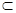 α,n α,n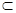  ,α∥ ,α∥ ,则m,n为异面直线 ,则m,n为异面直线 |
D.若α⊥ ,m⊥α,n⊥ ,m⊥α,n⊥ ,则m⊥n ,则m⊥n |
设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若m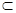 α,n α,n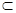 β,m∥n,则α∥β β,m∥n,则α∥β |
| B.若n⊥α,n⊥β,m⊥β,则m⊥α |
| C.若m∥α,n∥β,m⊥n,则α⊥β |
| D.若α⊥β,n⊥β,m⊥n,则m⊥α |
若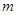 、
、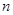 是两条不同的直线,
是两条不同的直线,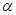 、
、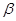 是两个不同的平面,则下列命题中不正确的是( )
是两个不同的平面,则下列命题中不正确的是( )
A.若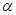 ∥ ∥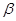 , ,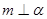 ,则 ,则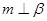 |
B.若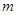 ∥ ∥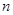 , ,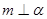 ,则 ,则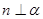 |
C.若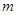 ∥ ∥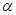 , ,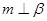 ,则 ,则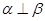 |
D.若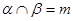 , ,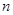 与 与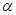 、 、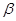 所成的角相等,则 所成的角相等,则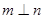 |
设m、n是两条不同的直线, 、β是两个不同的平面,则下列命题中正确的是
、β是两个不同的平面,则下列命题中正确的是
A.若m∥n,m∥ ,则n∥ ,则n∥ |
B.若 ⊥β,m∥ ⊥β,m∥ ,则m⊥β ,则m⊥β |
C.若 ⊥β,m⊥β,则m∥ ⊥β,m⊥β,则m∥ |
D.若m⊥n,m⊥ ,n⊥β,则 ,n⊥β,则 ⊥β ⊥β |
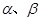 表示两个互相垂直的平面,
表示两个互相垂直的平面,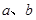 表示一对异面直线,则
表示一对异面直线,则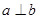 的一个充分条件是( )
的一个充分条件是( )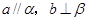 B.
B.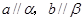
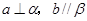 D.
D.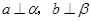
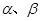 和两条不重合的直线
和两条不重合的直线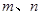 ,有下列四个命题:
,有下列四个命题: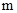 //
// ,
,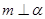 ,则
,则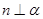 ; ②若
; ②若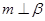 ,则
,则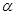 //
//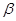 ;
; ,则
,则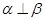 ; ④若
; ④若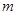 //
//