题目内容
已知椭圆C:
 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两焦点的距离之和为6.
,椭圆C上任意一点到椭圆两焦点的距离之和为6.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线
与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线 的方程.
的方程.

 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两焦点的距离之和为6.
,椭圆C上任意一点到椭圆两焦点的距离之和为6.(1)求椭圆C的方程;
(2)设直线
 与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线
与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线 的方程.
的方程.解 (1)由已知2a=6,=,解得a=3,c=,所以b2=a2-c2=3,故椭圆C的方程为+=1。
(2)设A(x1,y1),B(x2,y2),则AB的中点为E.
由得(1+3k2)x2-12kx+3=0,∵直线与椭圆有两个不同的交点,
∴Δ=144k2-12(1+3k2)>0,解得k2>.且x1+x2=,x1x2=.
而y1+y2=k(x1+x2)-4=k·-4=-,∴E点坐标为.
∵PA=PB,∴PE⊥AB,kPE·kAB=-1.∴·k=-1.解得k=±1,满足k2>,
∴直线l的方程为x-y-2=0或x+y+2=0.
(2)设A(x1,y1),B(x2,y2),则AB的中点为E.
由得(1+3k2)x2-12kx+3=0,∵直线与椭圆有两个不同的交点,
∴Δ=144k2-12(1+3k2)>0,解得k2>.且x1+x2=,x1x2=.
而y1+y2=k(x1+x2)-4=k·-4=-,∴E点坐标为.
∵PA=PB,∴PE⊥AB,kPE·kAB=-1.∴·k=-1.解得k=±1,满足k2>,
∴直线l的方程为x-y-2=0或x+y+2=0.
略

练习册系列答案
相关题目
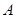 、
、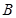 是椭圆
是椭圆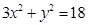 上的两点,点
上的两点,点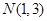 是线段
是线段 的中点,线段
的中点,线段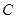 、
、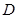 两点.
两点.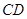 的中点
的中点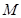 为圆心且与直线
为圆心且与直线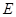 :
: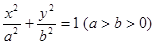 ,设该椭圆上的点到左焦点
,设该椭圆上的点到左焦点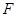
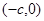 的最大距离为
的最大距离为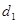 ,到右顶点
,到右顶点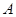
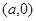 的最大距离为
的最大距离为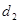 .
.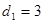 ,
,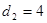 ,求椭圆
,求椭圆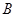
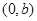 的最大距离为
的最大距离为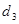 ,求证:
,求证: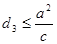 .
.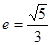 ,一条准线为
,一条准线为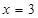 的椭圆的标准方程是________.
的椭圆的标准方程是________. 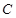 :
: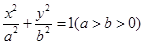 的离心率为
的离心率为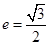 ,且过点
,且过点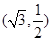 .
.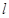 与椭圆
与椭圆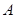 、
、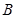 两点,若以
两点,若以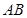 为直径的圆
为直径的圆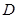 经过坐标原点.证明:圆
经过坐标原点.证明:圆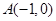 的直线
的直线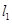 与过点
与过点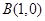 的直线
的直线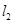 相交于点M,
相交于点M,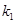 ,
,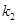 的乘积为定值
的乘积为定值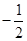 ,求点M的轨迹方程.
,求点M的轨迹方程. +
+  =1的焦点,P是曲线
=1的焦点,P是曲线 :
: 与C1的一个交点,则△PF1F2的面积为_____________
与C1的一个交点,则△PF1F2的面积为_____________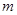 是两个正数
是两个正数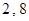 的等比中项,则圆锥曲线
的等比中项,则圆锥曲线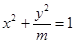 的离心率为 ( )
的离心率为 ( ) 或
或
