题目内容
设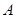 、
、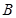 是椭圆
是椭圆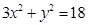 上的两点,点
上的两点,点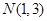 是线段
是线段 的中点,线段
的中点,线段 的垂直平分线与椭圆相交于
的垂直平分线与椭圆相交于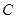 、
、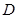 两点.
两点.
(Ⅰ)求直线 的方程;
的方程;
(Ⅱ)求以线段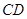 的中点
的中点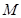 为圆心且与直线
为圆心且与直线 相切的圆的方程.
相切的圆的方程.
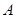 、
、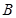 是椭圆
是椭圆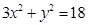 上的两点,点
上的两点,点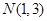 是线段
是线段 的中点,线段
的中点,线段 的垂直平分线与椭圆相交于
的垂直平分线与椭圆相交于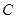 、
、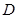 两点.
两点.(Ⅰ)求直线
 的方程;
的方程;(Ⅱ)求以线段
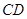 的中点
的中点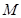 为圆心且与直线
为圆心且与直线 相切的圆的方程.
相切的圆的方程.(Ⅰ)法1:依题意显然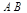 的斜率存在,可设直线
的斜率存在,可设直线 的方程为
的方程为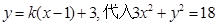 ,
,
整理得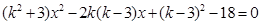 . ① ---------------2分
. ① ---------------2分
设 是方程①的两个不同的根,
是方程①的两个不同的根,
∴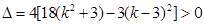 , ② --------4分
, ② --------4分
且 ,由
,由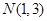 是线段
是线段 的中点,得
的中点,得
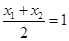 ,∴
,∴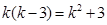 .
.
解得 ,这个值满足②式,
,这个值满足②式,
于是,直线 的方程为
的方程为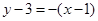 ,即
,即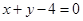 --------6分
--------6分
法2:设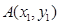 ,
,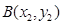 ,则有
,则有
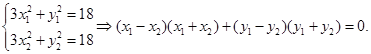 --------2分
--------2分
依题意,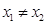 ,∴
,∴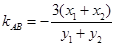 . ---------------------4分
. ---------------------4分
∵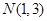 是
是 的中点, ∴
的中点, ∴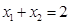 ,
,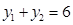 ,从而
,从而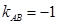 .
.
直线 的方程为
的方程为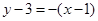 ,即
,即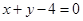 . ----------------6分
. ----------------6分
(Ⅱ)∵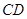 垂直平分
垂直平分 ,∴直线
,∴直线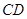 的方程为
的方程为 ,即
,即 ,
,
代入椭圆方程,整理得 . ③ ---------------8分
. ③ ---------------8分
又设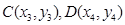 ,
,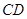 的中点为
的中点为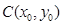 ,则
,则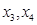 是方程③的两根,
是方程③的两根,
∴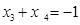 ,
,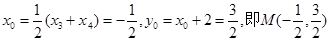 .-----10分
.-----10分
 到直线
到直线 的距离
的距离 ,故所求的以线段
,故所求的以线段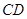 的中点
的中点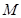 为圆心且与直线
为圆心且与直线 相切的圆的方程为:
相切的圆的方程为: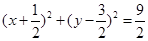
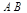 的斜率存在,可设直线
的斜率存在,可设直线 的方程为
的方程为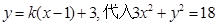 ,
,整理得
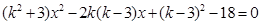 . ① ---------------2分
. ① ---------------2分设
 是方程①的两个不同的根,
是方程①的两个不同的根,∴
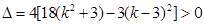 , ② --------4分
, ② --------4分且
 ,由
,由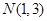 是线段
是线段 的中点,得
的中点,得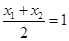 ,∴
,∴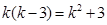 .
.解得
 ,这个值满足②式,
,这个值满足②式,于是,直线
 的方程为
的方程为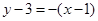 ,即
,即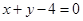 --------6分
--------6分法2:设
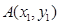 ,
,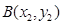 ,则有
,则有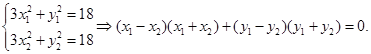 --------2分
--------2分依题意,
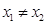 ,∴
,∴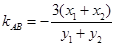 . ---------------------4分
. ---------------------4分∵
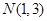 是
是 的中点, ∴
的中点, ∴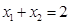 ,
,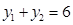 ,从而
,从而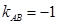 .
.直线
 的方程为
的方程为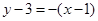 ,即
,即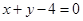 . ----------------6分
. ----------------6分(Ⅱ)∵
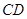 垂直平分
垂直平分 ,∴直线
,∴直线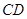 的方程为
的方程为 ,即
,即 ,
,代入椭圆方程,整理得
 . ③ ---------------8分
. ③ ---------------8分又设
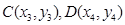 ,
,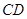 的中点为
的中点为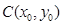 ,则
,则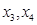 是方程③的两根,
是方程③的两根,∴
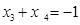 ,
,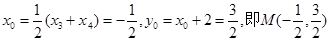 .-----10分
.-----10分 到直线
到直线 的距离
的距离 ,故所求的以线段
,故所求的以线段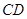 的中点
的中点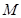 为圆心且与直线
为圆心且与直线 相切的圆的方程为:
相切的圆的方程为: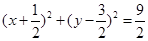
略

练习册系列答案
相关题目
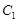 :
: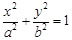 (
(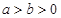 )的离心率为
)的离心率为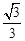 ,直线
,直线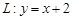 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆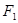 ,右焦点为
,右焦点为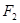 ,直线
,直线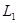 过点
过点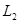 垂直
垂直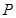 ,线段
,线段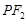 的垂直平分线交
的垂直平分线交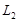 于点
于点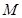 .
.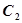 的方程;
的方程;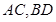 为点
为点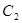 的过点
的过点 面积的最小值.
面积的最小值.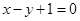 经过椭圆S:
经过椭圆S: 的一个焦点和一个顶点.
的一个焦点和一个顶点. 轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k. ,求证:
,求证: .
.

 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两焦点的距离之和为6.
,椭圆C上任意一点到椭圆两焦点的距离之和为6. 与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线
与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线 的方程.
的方程. +
+ =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程. 的焦点为
的焦点为 ,点p在椭圆上,若
,点p在椭圆上,若 ,则
,则
 的大小为
的大小为  上存在一点P,使得它对两个焦点
上存在一点P,使得它对两个焦点 ,
, 的张角
的张角 ,则该椭圆的离心率的取值范围是
,则该椭圆的离心率的取值范围是



 的曲线恰好有两个不同的公共点,则实数
的曲线恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是


 =1(a>b>0)的顶点(如图),直线l与椭圆交于异于顶点的P,Q两点,且l∥A2B,若椭圆的离心率是
=1(a>b>0)的顶点(如图),直线l与椭圆交于异于顶点的P,Q两点,且l∥A2B,若椭圆的离心率是 ,且|A2B|=
,且|A2B|= 。
。