题目内容
【题目】已知函数![]() .
.
(1)若![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试判断![]() 在
在![]() 内的单调性,并用定义证明.
内的单调性,并用定义证明.
【答案】(1)1(2)见解析
【解析】试题分析:(1)![]() ,由于函数
,由于函数![]() 为奇函数,所以有
为奇函数,所以有![]() ,即
,即![]() ,解得
,解得![]() ;(2)首先判断函数
;(2)首先判断函数![]() 在区间
在区间![]() 上单调递增,可以根据函数单调性定义进行证明,设
上单调递增,可以根据函数单调性定义进行证明,设![]() 是区间
是区间![]() 上任意两个不等的实数,且
上任意两个不等的实数,且![]() ,则
,则![]() ,
, 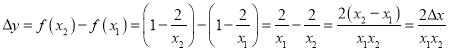 ,由于
,由于![]() 且
且![]() ,所以
,所以![]() ,即
,即![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
试题解析:(1)由已知g(x)=f(x)-a得,
g(x)=1-a-![]() ,
,
因为g (x)是奇函数,所以g(-x)=-g(x),
即1-a-![]() =-
=-![]() ,
,
解得a=1.
(2)函数f(x)在(0,+∞)内为增函数.
证明如下:
设x1、x2为(0,+∞)内的任意两点,且x1<x2,
则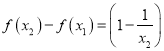
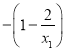
![]() .
.
因为0<x1<x2,所以![]() ,x1x2>0,
,x1x2>0,
从而![]() ,
,
即f(x1)<f(x2).
所以函数f(x)在(0,+∞)内是增函数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响,部分统计数据如下:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 |
|
| |
学习成绩不优秀 |
|
| |
合计 |
(1)根据以上统计数据,你是否有![]() 的把握认为使用智能手机对学习有影响?
的把握认为使用智能手机对学习有影响?
(2)为进一步了解学生对智能手机的使用习惯,现从全校使用智能手机的高中生中(人数很多)随机抽取 ![]() 人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
【题目】某市要对该市六年级学生进行体育素质调查测试,现让学生从“跳绳、短跑![]() 米、长跑
米、长跑![]() 米、仰卧起坐、游泳
米、仰卧起坐、游泳![]() 米、立定跳远”
米、立定跳远”![]() 项中选择
项中选择![]() 项进行测试,其中“短跑、长跑、仰卧起坐”
项进行测试,其中“短跑、长跑、仰卧起坐”![]() 项中至少选择其中
项中至少选择其中![]() 项进行测试.现从该市六年级学生中随机抽取了
项进行测试.现从该市六年级学生中随机抽取了![]() 名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中
名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中![]() )
)
选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数 |
|
|
|
人数 |
|
|
|
已知从所调查的![]() 名学生中任选
名学生中任选![]() 名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为
名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为![]() ,记
,记![]() 为这
为这![]() 名学生选择“短跑、长跑、仰卧起坐”的项目个数之和.
名学生选择“短跑、长跑、仰卧起坐”的项目个数之和.
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.


