题目内容
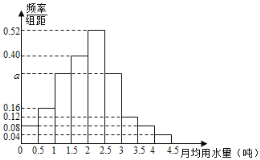
【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.

(I)求![]() 的值;
的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
【答案】(Ⅰ) ![]() (Ⅱ) 平均数74.9,众数75.14,中位数75;(Ш)
(Ⅱ) 平均数74.9,众数75.14,中位数75;(Ш) ![]()
【解析】
(I)根据频率之和为![]() 列方程,结合
列方程,结合![]() 求出
求出![]() 的值.(II)利用各组中点值乘以频率然后相加,求得平均数.利用中位数是面积之和为
的值.(II)利用各组中点值乘以频率然后相加,求得平均数.利用中位数是面积之和为![]() 的地方,列式求得中位数.以频率分布直方图最高一组的中点作为中位数.(III)先计算出从
的地方,列式求得中位数.以频率分布直方图最高一组的中点作为中位数.(III)先计算出从![]() ,
,![]() 中分别抽取
中分别抽取![]() 人和
人和![]() 人,再利用列举法和古典概型概率计算公式,计算出所求的概率.
人,再利用列举法和古典概型概率计算公式,计算出所求的概率.
解:(I)依题意得![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
(Ⅱ)平均数为![]()
中位数为![]()
众数为![]()
(Ш)依题意,知分数在![]() 的市民抽取了2人,记为
的市民抽取了2人,记为![]() ,分数在
,分数在![]() 的市民抽取了6人,记为1,2,3,4,5,6,
的市民抽取了6人,记为1,2,3,4,5,6,
所以从这8人中随机抽取2人所有的情况为:
![]() ,
,
![]() 共28种,
共28种,
其中满足条件的为![]() ,
,![]() 共13种,设“至少有1人的分数在
共13种,设“至少有1人的分数在![]() ”的事件为
”的事件为![]() ,则
,则![]()

练习册系列答案
相关题目