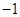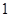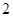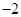题目内容
若函数y=ax+b-1(a>0且a≠1 )的图象经过一、三、四象限,则下列结论中正确的是( )
| A.a>1且b<1 | B.0<a<1 且b<0 |
| C.0<a<1 且b>0 | D.a>1 且b<0 |
D
试题分析:对于指数函数y=ax(a>o且a≠1),
分别在坐标系中画出当0<a<1和a>1时函数的图象如下:
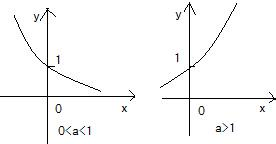
∵函数y=ax+b-1的图象经过第一、三、四象限,∴a>1,
由图象平移知,b-1<-1,解得b<0,
故选D.
点评:解决该试题的关键是先在坐标系中画出当0<a<1和a>1时指数函数的图象,由图得a>1,再由上下平移求出m的范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
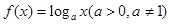 ,若
,若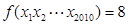 ,则
,则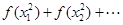
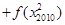 的值等于 .
的值等于 .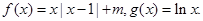 .
.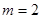 时,求函数
时,求函数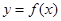 在
在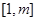 上的最大值;
上的最大值; ,若函数
,若函数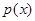 有零点,求
有零点,求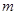 的取值范围.
的取值范围.  与每日生产产品件数
与每日生产产品件数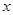 (
(
 )间的关系为
)间的关系为 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元. (元)表示成日产量
(元)表示成日产量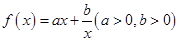 的单调性并给出证明。
的单调性并给出证明。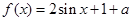 是一个奇函数.
是一个奇函数.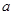 的值和
的值和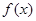 的值域;
的值域;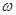 >
> ,若
,若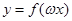 在区间
在区间 是增函数,求
是增函数,求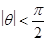 ,若对
,若对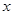 取一切实数,不等式
取一切实数,不等式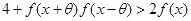 都成立,求
都成立,求 的取值范围.
的取值范围.
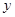 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里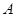 处,如图,现假设:①失事船的移动路径可视为抛物线
处,如图,现假设:①失事船的移动路径可视为抛物线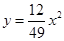 ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发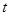 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为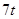

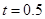 时,写出失事船所在位置
时,写出失事船所在位置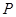 的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)
的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)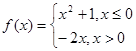 ,则
,则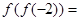 .
. 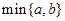 表示
表示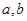 两个数中的最小的数,若函数
两个数中的最小的数,若函数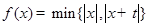 的图像关于直线
的图像关于直线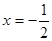 对称,则
对称,则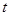 的值是( )
的值是( )