��Ŀ����
����Ŀ����ͼ����������һ��ֱ���õ�Բ�α�־�Բ��ΪC�������ĽӴ���ΪG����Բ�α�־����ͬһƽ���ڵĵ����ϵ�P����һ���۲�㣬��PG=50m���ڹ۲����ǰ��10m������PD=10m����һ����Ϊ10m����ED=10m���Ĺ������ס�����ߣ�����ڹ۲�����ܿ�����Բ�α�־����ּ�Ϊͼ�д�A��F��Բ���� 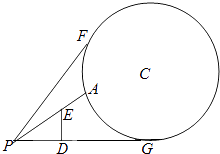
��1����Բ�α�־��뾶Ϊ25m����PG����ֱ��Ϊx�ᣬGΪ����ԭ�㣬����ֱ������ϵ����ԲC��ֱ��PF�ķ��̣�
��2�����ڵ�P���۲��Բ�α�־������ӽǣ�����APF��������ֵΪ ![]() �����Բ�α�־��İ뾶��
�����Բ�α�־��İ뾶��
���𰸡�
��1���⣺ԲC��x2+��y��25��2=252��
ֱ��PB���̣�x��y+50=0��
��ֱ��PF���̣�y=k��x+50����k��0����
��Ϊֱ��PF��ԲC���У����� ![]() �����
����� ![]()
����ֱ��PF���̣� ![]() ����4x��3y+200=0
����4x��3y+200=0
��2���⣺��ֱ��PF���̣�y=k��x+50����k��0����ԲC��x2+��y��r��2=r2��
��Ϊtan��APF=tan����GPF����GPA��= ![]() =
= ![]() ������
������ ![]()
����ֱ��PF���̣� ![]() ����40x��9y+2000=0��
����40x��9y+2000=0��
��Ϊֱ��PF��ԲC���У����� ![]() ��
��
�����2r2+45r��5000=0������2r+125����r��40��=0��
��r=40
����������1������Բ����뾶���ɵ�Բ�ķ��̣�����PF��ԲC���У��ɵ�ֱ��PF�ķ��̣���2�������ֱ��PF���̣�������ֱ��PF��ԲC���У������Բ�α�־��İ뾶��

 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�