题目内容
【题目】已知数列![]() 的前n项的和Sn,点(n,Sn)在函数
的前n项的和Sn,点(n,Sn)在函数![]() =2x2+4x图象上:
=2x2+4x图象上:
(1)证明![]() 是等差数列;
是等差数列;
(2)若函数![]() ,数列{bn}满足bn=
,数列{bn}满足bn=![]() ,记cn=anbn,求数列
,记cn=anbn,求数列![]() 前n项和Tn;
前n项和Tn;
(3)是否存在实数λ,使得当x≤λ时,f(x)=﹣x2+4x﹣![]() ≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
【答案】(1) 数列{an}的通项公式为an=4n+2;(2) Tn=10﹣(2n+5)![]() ;(3) 实数λ=1,见解析.
;(3) 实数λ=1,见解析.
【解析】试题分析:(1)要求数列的通项公式,利用![]() ,然后把
,然后把![]() 代入验证;
代入验证;
(2)由函数![]() ,数列
,数列![]() 满足
满足![]() ,利用错位相减法可得数列{
,利用错位相减法可得数列{![]() 前
前![]() 项和
项和![]()
(3)假设存在实数![]() ,使得当
,使得当![]() 时,
时,![]()
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,由
恒成立,由![]()
是递增数列,能推导出存在最大的实数![]() ,使得当
,使得当![]() 时,
时,![]() 对任意
对任意![]() 恒成立
恒成立
试题解析;(1)由题意,Sn=2n2+4n,
当n=1时,a1=S1=6,
![]() n≥2时,an=Sn﹣Sn﹣1=(2n2+4n)﹣[2(n﹣1)2+4(n﹣1)]=4n+2,
n≥2时,an=Sn﹣Sn﹣1=(2n2+4n)﹣[2(n﹣1)2+4(n﹣1)]=4n+2,
当n=1时,a1=S1=4+2=6,也适合上式
∴数列{an}的通项公式为an=4n+2,n∈N*;![]() 是等差数列
是等差数列
(2)∵函数g(x)=2﹣x,
∴数列{bn}满足bn=g(n)=2﹣n,
又∵cn=anbn,
∴Tn=6×2﹣1+10×2﹣2+14×2﹣3+…+(4n+2)×2﹣n,…①,
∴![]() Tn=6×2﹣2+10×2﹣3+…+(4n﹣2)×2﹣n+(4n+2)×2﹣(n+1),…②,
Tn=6×2﹣2+10×2﹣3+…+(4n﹣2)×2﹣n+(4n+2)×2﹣(n+1),…②,
①﹣②得:
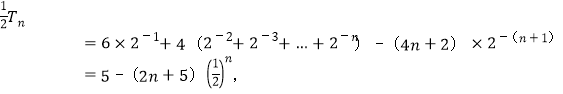
![]()
(3)假设存在实数λ,使得当x≤λ时,![]() 对任意
对任意
n∈N*恒成立,即![]() 任意n∈N*恒成立,
任意n∈N*恒成立,
∵an=4n+2,![]() 是递增数列,
是递增数列,
所以只要﹣x2+4x≤c1,即x2﹣4x+3≥0,解得x≤1或x≥3.
所以存在最大的实数λ=1,使得当x≤λ时,f(x)≤cn对任意n∈N*恒成立.

【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机购为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事用户车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.