题目内容
设抛物线y2=2px(p>0)上有两动点A、B,F为焦点,且|
|+|
|=8,且线段AB的垂直平分线恒过定点Q(6,0).
(1)求抛物线方程;
(2)求△AQB面积最大值.
| AF |
| BF |
(1)求抛物线方程;
(2)求△AQB面积最大值.
分析:(1)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),利用抛物线方程与直线的斜率公式,算出M的坐标关于AB斜率k和p的式子,根据AB的中垂线线恒过定点Q(6,0)利用斜率公式建立关于p的等式,解出p值即可得到抛物线方程;
(2)由抛物线方程和直线AB方程消去x,得y2-2y0y+2y02-16=0,从而算出|y1-y2|=
,由△AQB在x轴上截得的线段|QD|=4+
y02,得到△AQB面积S关于y0的表达式,再利用基本不等式求最值即可算出△AQB面积最大值.
(2)由抛物线方程和直线AB方程消去x,得y2-2y0y+2y02-16=0,从而算出|y1-y2|=
| 64-4y02 |
| 1 |
| 4 |
解答:解:(1)设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),
①当直线AB的斜率存在时,设斜率为k,则
由|AF|+|BF|=8得x1+x2+p=8,∴x0=4-
又∵y12=2px1且y22=2px2,∴y12-y22=2p(x1-x2)
可得k=
=
=
,解出y0=
,得M(4-
,
),
∵线段AB的垂直平分线恒过定点Q(6,0),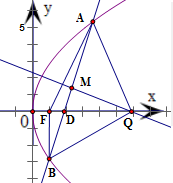
∴
•k=-1,解之得p=4,可得抛物线方程为y2=8x,
②当直线的斜率不存在时,可得|
|+|
|=2p=8,
也满足抛物线方程为y2=8x.
综上所述,可得抛物线方程为y2=8x;
(2)当直线的斜率存在时,由x0=4-
=2,得M(2,y0)
∵AB斜率k=
,∴直线AB方程为y-y0=
(x-2)
令y=0,解出直线与x轴的交点为D(2-
y02,0),
∵由y2=8x和y-y0=
(x-2)消去x,得:y2-2y0y+2y02-16=0,
∴|y1-y2|=
=
=
,
∵|QD|=6-(2-
y02)=4+
y02,
∴△AQB面积为S=
|QD|•|y1-y2|=
(4+
y02)•
=
∵
≤
=
,
∴S=
≤
•
=
.
当直线的斜率不存在时,直线AB的方程为x=2且|AB|=8,
可得△ABS面积S=
×8×4=16<
.
∴△AQB面积最大值为
.
①当直线AB的斜率存在时,设斜率为k,则
由|AF|+|BF|=8得x1+x2+p=8,∴x0=4-
| p |
| 2 |
又∵y12=2px1且y22=2px2,∴y12-y22=2p(x1-x2)
可得k=
| y1-y2 |
| x1-x2 |
| 2p |
| y1+y2 |
| p |
| y0 |
| p |
| k |
| p |
| 2 |
| p |
| k |
∵线段AB的垂直平分线恒过定点Q(6,0),

∴
| ||
4-
|
②当直线的斜率不存在时,可得|
| AF |
| BF |
也满足抛物线方程为y2=8x.
综上所述,可得抛物线方程为y2=8x;
(2)当直线的斜率存在时,由x0=4-
| p |
| 2 |
∵AB斜率k=
| p |
| y0 |
| p |
| y0 |
令y=0,解出直线与x轴的交点为D(2-
| 1 |
| 4 |
∵由y2=8x和y-y0=
| p |
| y0 |
∴|y1-y2|=
| (y1+y2)2-4y1y2 |
| 4y02-4(2y02-16) |
| 64-4y02 |
∵|QD|=6-(2-
| 1 |
| 4 |
| 1 |
| 4 |
∴△AQB面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 64-4y02 |
=
| 1 | ||
4
|
| (16+y02)(16+y02)(32-2y02) |
∵
| (16+y02)(16+y02)(32-2y02) |
[
|
512
| ||
| 9 |
∴S=
| 1 | ||
4
|
| (16+y02)(16+y02)(32-2y02) |
| 1 | ||
4
|
512
| ||
| 9 |
64
| ||
| 9 |
当直线的斜率不存在时,直线AB的方程为x=2且|AB|=8,
可得△ABS面积S=
| 1 |
| 2 |
64
| ||
| 9 |
∴△AQB面积最大值为
64
| ||
| 9 |
点评:本题给出抛物线满足的条件,求抛物线方程并求三角形面积的最大值.着重考查了抛物线的标准方程与简单几何性质、直线与圆锥曲线的位置关系和三角形面积求法等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
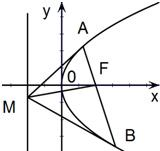 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)