题目内容
【题目】已知椭圆C: ![]() ,F1 , F2分别为左右焦点,在椭圆C上满足条件
,F1 , F2分别为左右焦点,在椭圆C上满足条件 ![]() 的点A有且只有两个
的点A有且只有两个
(1)求椭圆C的方程
(2)若过点F2的两条相互垂直的直线l1与l2 , 直线l1与曲线y2=4x交于两点M、N,直线l2与椭圆C交于两点P、Q,求四边形PMQN面积的取值范围.
【答案】
(1)解:∵在椭圆C上满足条件 ![]() 的点A有且只有两个,
的点A有且只有两个,
∴A点为椭圆短轴两端点,则b=c=1,∴a2=b2+c2=2,
则椭圆C的方程为: ![]()
(2)解:令M(x1,y1),N(x2,y2),当直线l1的斜率不存在时,直线l2的斜率为0,
求得|MN|=4,|PQ|=2 ![]() ,则
,则 ![]() ;
;
当直线l1的斜率存在时,设直线方程为y=k(x﹣1)(k≠0),
联立 ![]() ,得k2x2﹣(2k2+4)x+k2=0.
,得k2x2﹣(2k2+4)x+k2=0.
则 ![]() ,
,
|MN|= ![]() .
.
∵l1⊥l2,∴直线l2的方程:y=﹣ ![]() .
.
令P(x3,y3),Q(x4,y4),
联立 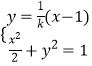 ,得(k2+2)x2﹣4x+2﹣2k2=0.
,得(k2+2)x2﹣4x+2﹣2k2=0.
![]() .
.
∴|PQ|= ![]() =
= ![]() .
.
∴ ![]() =
= ![]() .
.
令t=1+k2(t>1),
∴ ![]()
![]() .
.
∴四边形PMQN面积的取值范围是 ![]()
【解析】(1)由已知可得b=c=1,再由隐含条件求得a,则椭圆方程可求;(2)当直线l1的斜率不存在时,直线l2的斜率为0,求出|MN|、|PQ|,求出四边形的面积;当直线l1的斜率存在时,设直线方程为y=k(x﹣1)(k≠0),得到直线l2的方程:y=﹣ ![]() .分别联立直线方程与抛物线方程和椭圆方程,利用弦长公式求出|MN|、|PQ|,代入四边形面积公式,利用换元法求得四边形PMQN面积的取值范围.
.分别联立直线方程与抛物线方程和椭圆方程,利用弦长公式求出|MN|、|PQ|,代入四边形面积公式,利用换元法求得四边形PMQN面积的取值范围.

练习册系列答案
相关题目