题目内容
【题目】化简计算:
(1)化简: ![]() .
.
(2)已知:sinαcosα= ![]() ,且
,且 ![]() <α<
<α< ![]() ,求cosα﹣sinα的值.
,求cosα﹣sinα的值.
【答案】
(1)解:原式= 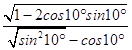 =
= ![]() =﹣1
=﹣1
(2)解:∵(sinα﹣cosα)2=sin2α﹣2sinαcosα+cos2α
=(sin2α+cos2α)﹣2sinαcosα;
又∵sin2α+cos2α=1,sinαcosα= ![]()
∴(sinα﹣cosα)2=1﹣2× ![]() =
= ![]()
∵ ![]() <α<
<α< ![]()
∴cosα﹣sinα=﹣ ![]()
【解析】(1)原式化简成平方和,即可求解;(2)根据sin2α+cos2α=1、完全平方差公式(a﹣b)2=a2﹣2ab+b2解答sinα﹣cosα的值即可.
【考点精析】掌握同角三角函数基本关系的运用是解答本题的根本,需要知道同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() .
.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目