题目内容
【题目】已知函数f(x)= ![]() sinxcosx﹣cos2x+
sinxcosx﹣cos2x+ ![]() ,(x∈R).
,(x∈R).
(1)若对任意x∈[﹣ ![]() ,
, ![]() ],都有f(x)≥a,求a的取值范围;
],都有f(x)≥a,求a的取值范围;
(2)若先将y=f(x)的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移 ![]() 个单位得到函数y=g(x)的图象,求函数y=g(x)﹣
个单位得到函数y=g(x)的图象,求函数y=g(x)﹣ ![]() 在区间[﹣2π,4π]内的所有零点之和.
在区间[﹣2π,4π]内的所有零点之和.
【答案】
(1)解:函数f(x)= ![]() sinxcosx﹣cos2x+
sinxcosx﹣cos2x+ ![]()
= ![]() sin2x﹣
sin2x﹣ ![]() cos2x=sin(2x﹣
cos2x=sin(2x﹣ ![]() ),
),
若对任意x∈[﹣ ![]() . ,
. , ![]() ],都有f(x)≥a,
],都有f(x)≥a,
则只需 f(x)min≥a即可.
∵2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ]当2x﹣
]当2x﹣ ![]() =﹣
=﹣ ![]() 时,
时,
f(x)min=﹣ ![]() ,故 a≤﹣
,故 a≤﹣ ![]() .
.
(2)解:若先将y=f(x)的图象上每个点纵坐标不变,
横坐标变为原来的2倍,可得y=sin(x﹣ ![]() )的图象;
)的图象;
然后再向左平移 ![]() 个单位得到函数y=g(x)=sinx的图象.
个单位得到函数y=g(x)=sinx的图象.
令g(x)﹣ ![]() =0,求得sinx=
=0,求得sinx= ![]() ,
,
求函数y=g(x)﹣ ![]() 在区间[﹣2π,4π]内的所有零点之和.
在区间[﹣2π,4π]内的所有零点之和.
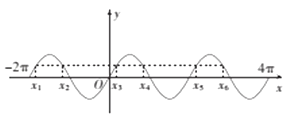
由图可知,sinx= ![]() 在区间[﹣2π,4π]内有6个零点:x1,x2,x3,x4,x5,x6,
在区间[﹣2π,4π]内有6个零点:x1,x2,x3,x4,x5,x6,
根据对称性有 ![]() =﹣
=﹣ ![]() ,
, ![]() =
= ![]() ,
, 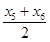 =
= ![]() ,
,
从而所有零点和为:x1+x2+x3+x4+x5+x6=3π.
【解析】(1)利用三角恒等变换化简f(x)的解析式,根据题意,x∈[﹣ ![]() ,
, ![]() ]时,f(x)min≥a.再利用正弦函数的定义域和值域,求得f(x)的最小值,可得a的范围.(2)根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,根据正弦函数的图象的对称性,求得函数y=g(x)﹣
]时,f(x)min≥a.再利用正弦函数的定义域和值域,求得f(x)的最小值,可得a的范围.(2)根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,根据正弦函数的图象的对称性,求得函数y=g(x)﹣ ![]() 在区间[﹣2π,4π]内的所有零点之和.
在区间[﹣2π,4π]内的所有零点之和.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 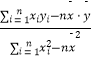 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.
