题目内容
三个人踢球,互相传递,每人每次只能踢一次,由甲开始踢,经过5次传递后,球又被踢回给甲,则不同的传递方式共有( )
| A.6种 | B.10种 | C.12种 | D.16种 |
B
根据题意,设在第n次传球后(n≥2),有 种情况球在甲手中,即经过n次传递后,球又被传回给甲,而前n次传球中,每次传球都有2种方法,则前n次传球的不同的传球方法共有
种情况球在甲手中,即经过n次传递后,球又被传回给甲,而前n次传球中,每次传球都有2种方法,则前n次传球的不同的传球方法共有 种,那么在第n次传球后,球不在甲手中的情况有
种,那么在第n次传球后,球不在甲手中的情况有 种情况,即球在乙或丙手中,只有在这些情况时,在第n+1次传球后,球才会被传回甲,即
种情况,即球在乙或丙手中,只有在这些情况时,在第n+1次传球后,球才会被传回甲,即 ;易得
;易得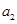 =2,则
=2,则 =
=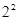 -2=2,
-2=2, =
=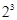 -2=6,
-2=6,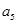 =
=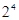 -6=10,
-6=10,
故选B,本题也可用树状图易得。
 种情况球在甲手中,即经过n次传递后,球又被传回给甲,而前n次传球中,每次传球都有2种方法,则前n次传球的不同的传球方法共有
种情况球在甲手中,即经过n次传递后,球又被传回给甲,而前n次传球中,每次传球都有2种方法,则前n次传球的不同的传球方法共有 种,那么在第n次传球后,球不在甲手中的情况有
种,那么在第n次传球后,球不在甲手中的情况有 种情况,即球在乙或丙手中,只有在这些情况时,在第n+1次传球后,球才会被传回甲,即
种情况,即球在乙或丙手中,只有在这些情况时,在第n+1次传球后,球才会被传回甲,即 ;易得
;易得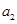 =2,则
=2,则 =
=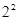 -2=2,
-2=2, =
=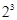 -2=6,
-2=6,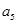 =
=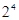 -6=10,
-6=10,故选B,本题也可用树状图易得。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目

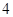 个小方格内,每格涂一种颜色,相邻(有公共边)两格涂不同的颜色,如果颜色可以反复使用,共有 种不同的涂色方法。
个小方格内,每格涂一种颜色,相邻(有公共边)两格涂不同的颜色,如果颜色可以反复使用,共有 种不同的涂色方法。  五人站成一排.求下列问题的排法总数;
五人站成一排.求下列问题的排法总数;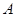 不站在排头也不站在排尾; (2)
不站在排头也不站在排尾; (2)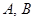 两人都不站在两端;
两人都不站在两端; 不站在排尾; (4)
不站在排尾; (4)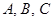 两两不相邻.
两两不相邻. 运算不产生进位现象,则称n为“给力数”.例如:32是 “给力数”,因为32 +33 +34不产生进位现象;23不是“给力数”,因为23 +24 +25产生进位现象.设小于1 000的所有“给力数”的各数位上的数字组成集合A,则用集合4中的数字可组成无重复数字的四位偶数的个数是________
运算不产生进位现象,则称n为“给力数”.例如:32是 “给力数”,因为32 +33 +34不产生进位现象;23不是“给力数”,因为23 +24 +25产生进位现象.设小于1 000的所有“给力数”的各数位上的数字组成集合A,则用集合4中的数字可组成无重复数字的四位偶数的个数是________