题目内容
8.设Sn为等比数列{an}的前n项和,已知3Sn=an+1-2,则公比q=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 分别令n=1,2建立方程关系即可得到结论.
解答 解:∵数列{an}是等比数列且3Sn=an+1-2,
∴3S1=a2-2,
3S2=a3-2,
两式相减得3S2-3S1=a3-a2,
即3a2=a3-a2,
即4a2=a3,
∴$\frac{{a}_{3}}{{a}_{2}}=4$,
即公比q=4,
故选:B
点评 本题主要考查等比数列通项公式的应用以及公比的求解,根据条件建立方程关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知直线ax+4y-2=0与2x-5y+b=0互相垂直,垂足为(1,c),则a+b+c的值为( )
| A. | -4 | B. | 20 | C. | 0 | D. | 24 |
16. 对某同学的6次数学测试成绩(满分100分)进行统计,作出如图所示茎叶图,给出关于该同学数学成绩的以下说法:①极差是12;②众数是85;③中位数是84;④平均数是85,正确的是( )
对某同学的6次数学测试成绩(满分100分)进行统计,作出如图所示茎叶图,给出关于该同学数学成绩的以下说法:①极差是12;②众数是85;③中位数是84;④平均数是85,正确的是( )
 对某同学的6次数学测试成绩(满分100分)进行统计,作出如图所示茎叶图,给出关于该同学数学成绩的以下说法:①极差是12;②众数是85;③中位数是84;④平均数是85,正确的是( )
对某同学的6次数学测试成绩(满分100分)进行统计,作出如图所示茎叶图,给出关于该同学数学成绩的以下说法:①极差是12;②众数是85;③中位数是84;④平均数是85,正确的是( )| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
13.下列函数中最小正周期为π且为偶函数的是( )
| A. | y=|sinx| | B. | y=tan$\frac{x}{2}$ | C. | y=-sin2x | D. | y=cos4x |
20.已知f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)-f(x)>0,对任意正数a、b,若a<b,则af(a),bf(b)的大小关系为( )
| A. | af(a)<bf(b) | B. | af(a)=bf(b) | C. | af(a)≤bf(b) | D. | af(a)≥bf(b) |
 已知平面四边形ABCD中,AB=8,BC=5,CD=3,AD=5,A+C=180°.
已知平面四边形ABCD中,AB=8,BC=5,CD=3,AD=5,A+C=180°. 的函数
的函数 ,若对任意的
,若对任意的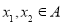 ,有
,有 ,则称函数
,则称函数 函数”,以下五个函数:①
函数”,以下五个函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ,其中是“定义上的
,其中是“定义上的 函数”的有( )
函数”的有( )