题目内容
20.已知f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)-f(x)>0,对任意正数a、b,若a<b,则af(a),bf(b)的大小关系为( )| A. | af(a)<bf(b) | B. | af(a)=bf(b) | C. | af(a)≤bf(b) | D. | af(a)≥bf(b) |
分析 令g(x)=$\frac{f(x)}{x}$,[x∈(0,+∞)],利用导数研究其单调性,再利用不等式的性质即可得出.
解答 解:令g(x)=$\frac{f(x)}{x}$,[x∈(0,+∞)],
∵xf′(x)-f(x)>0,
则g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$>0,
∴函数g(x)在x∈(0,+∞)单调递增,
∵a<b,∴$\frac{f(a)}{a}$<$\frac{f(b)}{b}$,
∴bf(a)<af(b),
∴af(a)<bf(a)<af(b)<bf(b).
故选:A.
点评 本题考查了利用导数研究其单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知函数f(x)=$\left\{\begin{array}{l}\frac{1}{x}-1,x>1\\-2x+a,x≤1\end{array}$在R上满足:对任意x1≠x2,都有f(x1)≠f(x2),则实数a的取值范围是( )
| A. | (-∞,2] | B. | (-∞,-2] | C. | [2,+∞) | D. | [-2,+∞) |
8.设Sn为等比数列{an}的前n项和,已知3Sn=an+1-2,则公比q=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
12.以下是解决数学问题的思维过程的流程

图中①、②两条流程线与“推理与证明”中的思维方法相匹配是( )

图中①、②两条流程线与“推理与证明”中的思维方法相匹配是( )
| A. | ①-分析法,②-反证法 | B. | ①-分析法,②-综合法 | ||
| C. | ①-综合法,②反证法 | D. | ①-综合法,②-分析法 |
 ,且
,且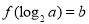 ,
, .
. 的最小值及对应的
的最小值及对应的 值;
值;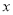 取何值时,
取何值时, ,且
,且 .
. 的单调性,并证明当
的单调性,并证明当 时,
时, ;
; 时,函数
时,函数 有最小值.设
有最小值.设 的最小值为
的最小值为 ,求函数
,求函数