题目内容
13.已知数列{an}满足:a1=$\frac{1}{2}$,$\frac{1}{{{a_{n+1}}}}=\frac{1}{{a_n^2+{a_n}}}$用[x]表示不超过x的最大整数,则$[\frac{1}{{{a_1}+1}}+\frac{1}{{{a_2}+1}}+…+\frac{1}{{{a_{2015}}+1}}]$的值等于( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由题意说明数列的项为正,利用裂项法化简数列递推关系式,进行求和即可.
解答 解:由题意可知an>0,
∵$\frac{1}{{{a_{n+1}}}}=\frac{1}{{a_n^2+{a_n}}}$=$\frac{1}{{a}_{n}({a}_{n}+1)}$=$\frac{1}{{a}_{n}}$-$\frac{1}{1+{a}_{n}}$,
即$\frac{1}{1+{a}_{n}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$,
则$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}$+…+$\frac{1}{{a}_{2015}+1}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$$-\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{2015}}$-$\frac{1}{{a}_{2016}}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2016}}$<$\frac{1}{{a}_{1}}$=2,
∵a1=$\frac{1}{2}$,
∴$\frac{1}{{a}_{2}}$=$\frac{1}{\frac{1}{4}+\frac{1}{2}}=\frac{1}{\frac{3}{4}}$,∴a2=$\frac{3}{4}$,同理a3=$\frac{16}{21}$,
则$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}$=$\frac{2}{3}+\frac{4}{7}$>1,
则1<$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}$+…+$\frac{1}{{a}_{2015}+1}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$$-\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{2015}}$-$\frac{1}{{a}_{2016}}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2016}}$<2,
则[$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}$+…+$\frac{1}{{a}_{2015}+1}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$$-\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{2015}}$-$\frac{1}{{a}_{2016}}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2016}}$]=1,
故选:B.
点评 本题考查数列的递推关系式的应用,新定义的应用,确定表达式的取值范围是解题的关键,考查分析问题解决问题的能力,转化思想的应用.

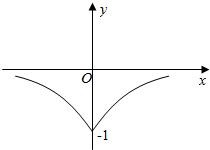
| A. | y=f(|x|) | B. | y=-|f(x)| | C. | y=-f(-|x|) | D. | y=f(-|x|) |
| A. | 10 | B. | 12 | C. | 10π | D. | 12π |
| A. | 年收入平均数大大增大,中位数一定变大,方差可能不变 | |
| B. | 年收入平均数大大增大,中位数可能不变,方差变大 | |
| C. | 年收入平均数大大增大,中位数可能不变,方差也不变 | |
| D. | 年收入平均数可能不变,中位数可能不变,方差可能不变 |
| A. | f(x)的图象过点(0,$\frac{1}{2}$) | B. | f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是减函数 | ||
| C. | f(x)的一个对称中心是($\frac{5π}{12}$,0) | D. | f(x)的图象的一条对称轴是x=$\frac{5π}{12}$ |
| A. | -$\frac{1}{2}$+π | B. | $\frac{5}{2}$-π | C. | $\frac{8}{3}$-π | D. | -$\frac{4}{3}$+π |